题目内容
在
+
=1中的“
| 4 |
| - |
| 9 |
| - |
10，15
10，15
”处分别填上一个自然数，并使它们的和最小10
10
15
15
．分析：若分别填上自然数a，b，则a，b满足
+
=1，它们的和a+b=（a+b）•1=（a+b）•（
+
）=）=13+
+
，可利用基本不等式研究最小值及求出a，b的值．
| 4 |
| a |
| 9 |
| b |
| 4 |
| a |
| 9 |
| b |
| 4b |
| a |
| 9a |
| b |
解答：解：设应分别填上自然数a，b，则
+
=1①，它们的和a+b=（a+b）•1=（a+b）•（
+
）=13+
+
≥13+2
=25，
当且仅当
=
，b=
a②时取等号，将①代入②解得a=10，∴b=15．
故答案为：10，15．
| 4 |
| a |
| 9 |
| b |
| 4 |
| a |
| 9 |
| b |
| 4b |
| a |
| 9a |
| b |
|
当且仅当
| 4b |
| a |
| 9a |
| b |
| 3 |
| 2 |
故答案为：10，15．
点评：本题考查基本不等式的应用：求最值．将a+b写成（a+b）•1，再将1代换成
+
创造基本不等式适用的形式是本解法的关键．读者应体会掌握这一题型及方法．基本不等式求最值时要注意三个原则：一正，即各项的取值为正；二定，即各项的和或积为定值；三相等，即要保证取等号的条件成立．
| 4 |
| a |
| 9 |
| b |
练习册系列答案
阅读快车系列答案
相关题目
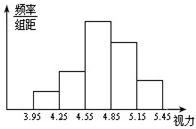中小学生的视力状况受到全社会的广泛关注，某市有关部门对全市3万名高中生的视力状况进行一次抽样调查统计，所得到的有关数据绘制成频率分布直方图，如图，从左至右五个小组的频率之比依次是2：4：9：7：3，第五小组的频数是36．
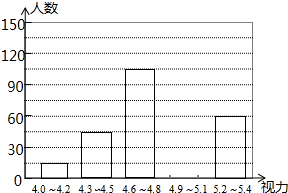为进一步加强中小学生近视眼的防控工作，市教育局近期下发了有关文件，将学生视力保护工作纳入学校和教师的考核内容，为此，某县教育组管部门对今年初中毕业生的视力进行了一次抽样调查，并根据调查结果绘制如下频数分布表和频数分布直方图的一部分．