题目内容
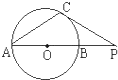
（几何证明选做题）若A，B，C是⊙O上三点，PC切⊙O于点C，∠ABC=110°，∠BCP=40°，则∠AOB的大小为______．
∵PC切⊙O于点C，OC为圆的半径
∴OC⊥PC，即∠PCO=90°
∵∠BCP=40°∴∠BCO=50°
由弦切角定理及圆周角定理可知，∠BOC=2∠PCB=80°
∵△BOC中，∠OBC=50°，∠ABC=110°
∴∠OBA=60°
∵OB=OA
∴∠AOB=60°
故答案为：60°
∴OC⊥PC，即∠PCO=90°
∵∠BCP=40°∴∠BCO=50°
由弦切角定理及圆周角定理可知，∠BOC=2∠PCB=80°
∵△BOC中，∠OBC=50°，∠ABC=110°
∴∠OBA=60°
∵OB=OA
∴∠AOB=60°
故答案为：60°
练习册系列答案
名校通行证有效作业系列答案
相关题目
（2013•惠州一模）（几何证明选做题）
（2012•昌平区一模）（几何证明选做题）若A，B，C是⊙O上三点，PC切⊙O于点C，∠ABC=110°，∠BCP=40°，则∠AOB的大小为
