题目内容
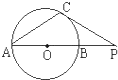
(几何证明选做题)若A,B,C是⊙O上三点,PC切⊙O于点C,∠ABC=110°,∠BCP=40°,则∠AOB的大小为 .
【答案】分析:由PC切⊙O于点C,OC为圆的半径可得∠PCO=90°,由∠BCP=40°,可求得∠BCO=50°,,由弦切角定理及圆周角定理可知,∠BOC=2∠PCB=80°,然后在△BOC中,由∠OBC=50°,∠ABC=110°可求∠OBA,进而可求
解答:解:∵PC切⊙O于点C,OC为圆的半径
∴OC⊥PC,即∠PCO=90°
∵∠BCP=40°∴∠BCO=50°
由弦切角定理及圆周角定理可知,∠BOC=2∠PCB=80°
∵△BOC中,∠OBC=50°,∠ABC=110°
∴∠OBA=60°
∵OB=OA
∴∠AOB=60°
故答案为:60°
点评:本题主要考查了圆的弦切角定理与圆周角定理的综合应用,灵活应用圆的基本定理是解答本题的关键
解答:解:∵PC切⊙O于点C,OC为圆的半径
∴OC⊥PC,即∠PCO=90°
∵∠BCP=40°∴∠BCO=50°
由弦切角定理及圆周角定理可知,∠BOC=2∠PCB=80°
∵△BOC中,∠OBC=50°,∠ABC=110°
∴∠OBA=60°
∵OB=OA
∴∠AOB=60°
故答案为:60°
点评:本题主要考查了圆的弦切角定理与圆周角定理的综合应用,灵活应用圆的基本定理是解答本题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题) (2012•昌平区一模)(几何证明选做题)若A,B,C是⊙O上三点,PC切⊙O于点C,∠ABC=110°,∠BCP=40°,则∠AOB的大小为
(2012•昌平区一模)(几何证明选做题)若A,B,C是⊙O上三点,PC切⊙O于点C,∠ABC=110°,∠BCP=40°,则∠AOB的大小为
