题目内容
已知函数![]() ,设曲线
,设曲线![]() 在与x轴交点处的切线为
在与x轴交点处的切线为![]() ,
,![]() 为
为![]() 的导函数,满足
的导函数,满足![]() .
.
(1)求![]() ;
;
(2)设![]() ,m>0,求函数
,m>0,求函数![]() 在[0,m]上的最大值;
在[0,m]上的最大值;
(3)设![]() ,若对于一切
,若对于一切![]() ,不等式
,不等式![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
(1)![]() ,
,
∵![]() ,∴函数
,∴函数![]() 的图象关于直线x=1对称b=-1,-----2分
的图象关于直线x=1对称b=-1,-----2分
∵曲线![]() 在与x轴交点处的切线为
在与x轴交点处的切线为![]() ,∴切点为(3,0),
,∴切点为(3,0),
∴![]() ,解得c=1,d=-3,则
,解得c=1,d=-3,则![]() ----------------5分
----------------5分
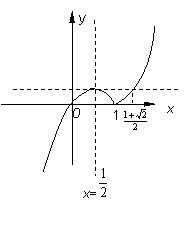 (2)∵
(2)∵![]() ,
,
∴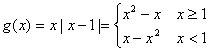 --------------------------7分
--------------------------7分
当0<m≤![]() 时,
时,![]()
当![]() <m≤
<m≤![]() 时,
时,![]() ,
,
当m>![]() 时,
时,![]() ,
,
综上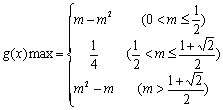 ----------------------------------10分
----------------------------------10分
(3)![]() ,
,![]() ,
,![]()
当![]() 时,|2x+1|=2x+1,所以不等式等价于
时,|2x+1|=2x+1,所以不等式等价于![]() 恒成立,
恒成立,
解得![]() ,且x≠t,--------------------------------------------13分
,且x≠t,--------------------------------------------13分
由![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() ,
,
又x≠t,∵ ![]() ,∴所求的实数t的的取值范围是
,∴所求的实数t的的取值范围是![]() -------16分
-------16分

练习册系列答案
相关题目
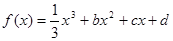 ,设曲线
,设曲线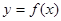 在与
在与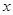 轴交点处的切线为
轴交点处的切线为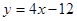 ,
,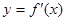 为
为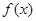 的导函数,满足
的导函数,满足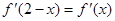 .
.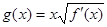 ,
,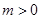 ,求函数
,求函数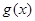 在
在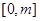 上的最大值;
上的最大值;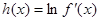 ,若对于一切
,若对于一切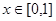 ,不等式
,不等式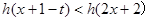 恒成立,求实数
恒成立,求实数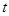 的取值范围.
的取值范围.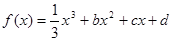 ,设曲线
,设曲线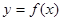 在与
在与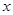 轴交点处的切线为
轴交点处的切线为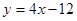 ,
,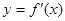 为
为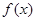 的导函数,满足
的导函数,满足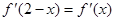 .
.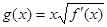 ,
,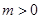 ,求函数
,求函数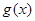 在
在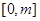 上的最大值;
上的最大值;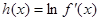 ,若对于一切
,若对于一切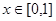 ,不等式
,不等式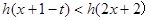 恒成立,求实数
恒成立,求实数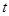 的取值范围.
的取值范围.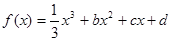 ,设曲线
,设曲线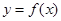 在与
在与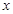 轴交点处的切线为
轴交点处的切线为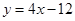 ,
,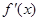 为
为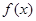 的导函数,满足
的导函数,满足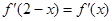 .
.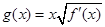 ,
,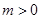 ,求函数
,求函数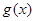 在
在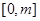 上的最大值;
上的最大值;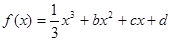 ,设曲线
,设曲线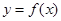 在与
在与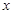 轴交点处的切线为
轴交点处的切线为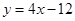 ,
,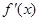 为
为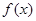 的导函数,满足
的导函数,满足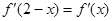 .
.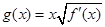 ,
,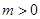 ,求函数
,求函数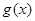 在
在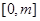 上的最大值;
上的最大值;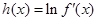 ,若对一切
,若对一切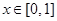 ,不等式
,不等式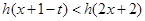 恒成立,求实数
恒成立,求实数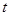 的取值范围.
的取值范围.