题目内容
已知函数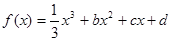 ,设曲线
,设曲线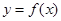 在与
在与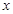 轴交点处的切线为
轴交点处的切线为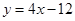 ,
,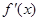 为
为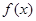 的导函数,满足
的导函数,满足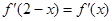 .
.
(1)求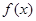 的单调区间.
的单调区间.
(2)设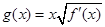 ,
,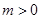 ,求函数
,求函数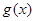 在
在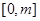 上的最大值;
上的最大值;
【答案】
(1)(2)
【解析】
试题分析:(1) ,
,
 ,
,
 函数
函数 的图像关于直线
的图像关于直线 对称,则
对称,则 .
.
 直线
直线 与
与 轴的交点为
轴的交点为 ,
,
 ,且
,且 ,
,
即 ,且
,且 ,解得
,解得 ,
, .
.
则 .
.
故 ,所以f(x)在R上单调递增. ……4分
,所以f(x)在R上单调递增. ……4分
(2)
其图像如图所示.当 时,
时, ,
,
根据图像得:

(ⅰ)当 时,
时, 最大值为
最大值为 ;
;
(ⅱ)当 时,
时, 最大值为
最大值为 ;
;
(ⅲ)当 时,
时, 最大值为
最大值为 . ……10分
. ……10分
考点:本小题主要考查导数的应用.
点评:用导数可以解决函数中求最值,单调性,极值等问题,要注意函数的定义域.分类讨论时,要注意分类标准要不重不漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
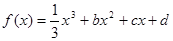 ,设曲线
,设曲线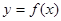 在与
在与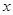 轴交点处的切线为
轴交点处的切线为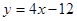 ,
,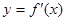 为
为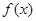 的导函数,满足
的导函数,满足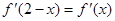 .
.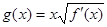 ,
,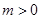 ,求函数
,求函数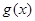 在
在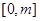 上的最大值;
上的最大值;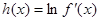 ,若对于一切
,若对于一切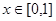 ,不等式
,不等式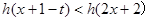 恒成立,求实数
恒成立,求实数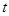 的取值范围.
的取值范围.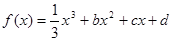 ,设曲线
,设曲线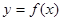 在与
在与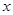 轴交点处的切线为
轴交点处的切线为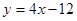 ,
,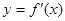 为
为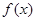 的导函数,满足
的导函数,满足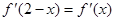 .
.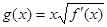 ,
,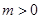 ,求函数
,求函数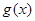 在
在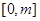 上的最大值;
上的最大值;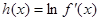 ,若对于一切
,若对于一切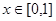 ,不等式
,不等式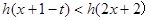 恒成立,求实数
恒成立,求实数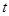 的取值范围.
的取值范围.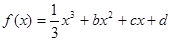 ,设曲线
,设曲线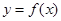 在与
在与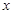 轴交点处的切线为
轴交点处的切线为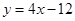 ,
,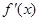 为
为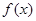 的导函数,满足
的导函数,满足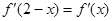 .
.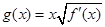 ,
,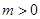 ,求函数
,求函数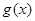 在
在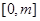 上的最大值;
上的最大值;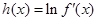 ,若对一切
,若对一切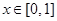 ,不等式
,不等式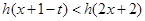 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.