Question

【题目】如图，四棱柱ABCD﹣A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，过A1、C、D三点的平面记为α，BB1与α的交点为Q．

（1）证明：Q为BB1的中点；
（2）若AA1=4，CD=2，梯形ABCD的面积为6，∠ADC=60°，求平面α与底面ABCD所成锐二面角的大小．

Answer 1

【答案】
（1）证明：Ⅰ∵BQ∥AA1，BC∥AD，

BC∩BQ=B，AD∩AA1=A，

∴平面QBC∥平面A1AD，

∴平面A1CD与这两个平面的交线相互平行，

即QC∥A1D．

∴△QBC与△A1AD的对应边相互平行，

∴△QBC∽△A1AD，

∴ ，

∴Q为BB1的中点．

（2）解法一：如图1所示，在△ADC中，作AE⊥DC，垂足为E，连接A1E．

又DE⊥AA1，且AA1∩AE=A，

所以DE⊥平面AEA1，所以DE⊥A1E．

所以∠AEA1为平面α与底面ABCD所成二面角的平面角．

因为BC∥AD，AD=2BC，所以S△ADC=2S△BCA．

又因为梯形ABCD的面积为6，DC=2，

所以S△ADC=4，AE=4．

于是tan∠AEA1= =1，∠AEA1= ．

故平面α与底面ABCD所成二面角的大小为 ．

解法二：如图2所示，

以D为原点，DA，DD1分别为x轴和z轴正方向建立空间直角坐标系．

设∠CDA=θ，BC=a，则AD=2a．

因为S四边形ABCD= 2sin60°=6，

所以a= ．

从而可得C（1， ，0），A1（ ，0，4），

所以DC=（1， ，0）， =（ ，0，4）．

设平面A1DC的法向量 =（x，y，1），

由 ，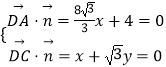

得 ，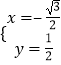

所以 =（﹣ ， ，1）．

又因为平面ABCD的法向量 =（0，0，1），

所以cos＜ ， ＞= = ，

故平面α与底面ABCD所成二面角的大小为 ．

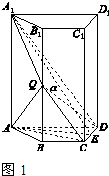
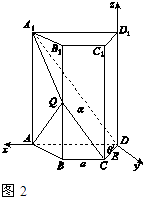
【解析】（1）由已知得平面QBC∥平面A1AD，从而QC∥A1D，由此能证明Q为BB1的中点．（2）法一：在△ADC中，作AE⊥DC，垂足为E，连接A1E，∠AEA1为平面α与底面ABCD所成二面角的平面角，由此求出平面α与底面ABCD所成二面角的大小．（3）法二：以D为原点，DA，DD1分别为x轴和z轴正方向建立空间直角坐标系，由此利用向量法能求出平面α与底面ABCD所成二面角的大小．