题目内容
已知ABCD是边长为2的正方形,E、F分别是BC、CD的中点,则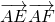 =
=
- A.6
- B.5
- C.4
- D.3
C
分析:根据直角三角形中的边角关系求得 tan∠EAN 和tan∠FAD 的值,由两角和的正切公式求得tan(∠EAB+∠FAD) 的值,
进而利用诱导公式求得 tan∠EAF,进而求得cos∠EAF的值,由此求得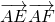 =AE•AF•cos∠EAF 的值.
=AE•AF•cos∠EAF 的值.
解答:由题意可得 AE=AF= =
= ,tan∠EAN=tan∠FAD=
,tan∠EAN=tan∠FAD= ,
,
∴tan(∠EAB+∠FAD)= =
= =
= ,
,
∴tan∠EAF=tan[90°-(∠EAB+∠FAD)]=cot(∠EAB+∠FAD)= .
.
故cos∠EAF= ,
,
则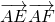 =AE•AF•cos∠EAF=
=AE•AF•cos∠EAF= •
• •
• =4,
=4,
故选C.
点评:本题主要考查两个向量的数量积的定义,直角三角形中的边角关系,两角和的正切公式,诱导公式,同角三角函数
的基本关系,属于中档题.
分析:根据直角三角形中的边角关系求得 tan∠EAN 和tan∠FAD 的值,由两角和的正切公式求得tan(∠EAB+∠FAD) 的值,
进而利用诱导公式求得 tan∠EAF,进而求得cos∠EAF的值,由此求得
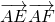 =AE•AF•cos∠EAF 的值.
=AE•AF•cos∠EAF 的值.解答:由题意可得 AE=AF=
 =
= ,tan∠EAN=tan∠FAD=
,tan∠EAN=tan∠FAD= ,
,∴tan(∠EAB+∠FAD)=
 =
= =
= ,
,∴tan∠EAF=tan[90°-(∠EAB+∠FAD)]=cot(∠EAB+∠FAD)=
 .
.故cos∠EAF=
 ,
,则
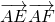 =AE•AF•cos∠EAF=
=AE•AF•cos∠EAF= •
• •
• =4,
=4,故选C.
点评:本题主要考查两个向量的数量积的定义,直角三角形中的边角关系,两角和的正切公式,诱导公式,同角三角函数
的基本关系,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
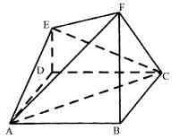 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.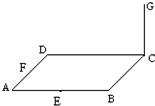 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离. 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.