题目内容
解不等式:
(1)
(2)(x+1)(x2-x+6)≥0.
解:(1)∵ ,
,
∴ ,即
,即 ,
, ,
,
∴-x(x+1)<0,x(x+1)>0
∴原不等式的解集为{x|x>0或x<-1}
(2)∵x2-x+6= +
+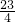 >0,
>0,
∴(x+1)(x2-x+6)≥0?x+1≥0,
∴原不等式的解集为{x|x≥-1}
分析:(1)将 右端中的1移向到左端,再通分解答即可;
右端中的1移向到左端,再通分解答即可;
(2)由于x2-x+6>0恒成立,于是问题即可解决.
点评:本题考查其他不等式的解法,关键在于转化为一端为乘积,另一端为0,再用不等式的性质解决,属于基础题.
 ,
,∴
 ,即
,即 ,
, ,
,∴-x(x+1)<0,x(x+1)>0
∴原不等式的解集为{x|x>0或x<-1}
(2)∵x2-x+6=
 +
+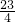 >0,
>0,∴(x+1)(x2-x+6)≥0?x+1≥0,
∴原不等式的解集为{x|x≥-1}
分析:(1)将
 右端中的1移向到左端,再通分解答即可;
右端中的1移向到左端,再通分解答即可;(2)由于x2-x+6>0恒成立,于是问题即可解决.
点评:本题考查其他不等式的解法,关键在于转化为一端为乘积,另一端为0,再用不等式的性质解决,属于基础题.

练习册系列答案
相关题目
 (2)
(2)
 (2)
(2)