题目内容
如图,在△ABC中,∠C=90°,AC=8,BC=6.P是AB边上的一个动点(异于A、B两点),过点P分别作AC、BC边的垂线,垂足为M、N.设AP=x.
(1)在△ABC中,AB=______;
(2)当x=______时,矩形PMCN的周长是14;
(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断,并加以说明.

(1)在△ABC中,AB=______;
(2)当x=______时,矩形PMCN的周长是14;
(3)是否存在x的值,使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断,并加以说明.

(1)∵△ABC中,∠C=90°,AC=8,BC=6.
∴AB=
=10
(2)若AP=x,则MC=PN=
(10-x),MP=CN=
x
则矩形PMCN的周长为16-
x
又∵矩形PMCN的周长是14
∴x=5
(3)∵AP=x,
∴△PAM的面积S△PAM=
x2,
△PBN的面积S△PBN=
(10-x)2,
矩形PMCN的面积SPMCN=
x(10-x)
若S△PAM=S△PBN,则x2=(10-x)2,解得,x=5;
若S△PAM=SPMCN,则x2=2x(10-x),即x=
,
故不存在x的值,使△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等
∴AB=
| AC2+BC2 |
(2)若AP=x,则MC=PN=
| 4 |
| 5 |
| 3 |
| 5 |
则矩形PMCN的周长为16-
| 2 |
| 5 |
又∵矩形PMCN的周长是14
∴x=5
(3)∵AP=x,
∴△PAM的面积S△PAM=
| 6 |
| 25 |

△PBN的面积S△PBN=
| 6 |
| 25 |
矩形PMCN的面积SPMCN=
| 12 |
| 25 |
若S△PAM=S△PBN,则x2=(10-x)2,解得,x=5;
若S△PAM=SPMCN,则x2=2x(10-x),即x=
| 20 |
| 3 |
故不存在x的值,使△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =40;
=40; 分)如图,已知梯形
分)如图,已知梯形 中,
中,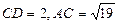 ,
, 。求梯形的高.
。求梯形的高.
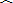
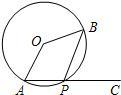




 ,动点
,动点 是
是 内的点,
内的点, ,若四边形
,若四边形 的面积等于
的面积等于 ,则线段
,则线段 的长度的最小值等于
的长度的最小值等于 