题目内容
椭圆 的焦点F1,F2,P为椭圆上的一点,已知PF1⊥PF2,则△F1PF2的面积为
的焦点F1,F2,P为椭圆上的一点,已知PF1⊥PF2,则△F1PF2的面积为
- A.8
- B.9
- C.10
- D.12
B
分析:先设出|PF1|=m,|PF2|=n,利用椭圆的定义求得n+m的值,平方后求得mn和m2+n2的关系,代入△F1PF2的勾股定理中求得mn的值,即可求出△F1PF2的面积.
解答:设|PF1|=m,|PF2|=n,
由椭圆的定义可知m+n=2a,
∴m2+n2+2nm=4a2,
∴m2+n2=4a2-2nm
由勾股定理可知
m2+n2=4c2,
求得mn=18,
则△F1PF2的面积为9.
故选B.
点评:本题主要考查了椭圆的应用,椭圆的简单性质和椭圆的定义.考查了考生对所学知识的综合运用.
分析:先设出|PF1|=m,|PF2|=n,利用椭圆的定义求得n+m的值,平方后求得mn和m2+n2的关系,代入△F1PF2的勾股定理中求得mn的值,即可求出△F1PF2的面积.
解答:设|PF1|=m,|PF2|=n,
由椭圆的定义可知m+n=2a,
∴m2+n2+2nm=4a2,
∴m2+n2=4a2-2nm
由勾股定理可知
m2+n2=4c2,
求得mn=18,
则△F1PF2的面积为9.
故选B.
点评:本题主要考查了椭圆的应用,椭圆的简单性质和椭圆的定义.考查了考生对所学知识的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
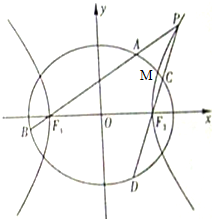 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆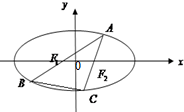 椭圆
椭圆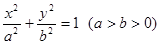 的焦点F1,F2,短轴长为8,离心率为
的焦点F1,F2,短轴长为8,离心率为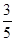 ,过F1的直线交椭圆于A、B两点,则
,过F1的直线交椭圆于A、B两点,则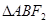 的周长为( )
的周长为( )