题目内容
已知函数f(x)= x2+
x2+ x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式an;
(2)令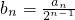 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)令cn= +
+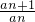 ,证明:2n<c1+c2+…+cn<2n+
,证明:2n<c1+c2+…+cn<2n+ .
.
解:(1)∵点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴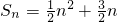 ,
,
∴当n=1时, ;
;
当n≥2时,an=Sn-Sn-1=
 .
.
当n=1时,也适合上式,
因此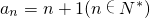 .
.
(2)由(1)可得: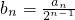 =
= .
.
∴Tn= ,
,
 ,
,
两式相减得 =1+
=1+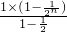
 =3
=3
∴ .
.
(3)证明:由cn=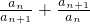 =
= +
+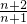 >2
>2 =2,
=2,
∴c1+c2+…+cn>2n.
又cn= +
+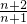 =2+
=2+ -
- ,
,
∴c1+c2+…+cn=2n+[( -
- )+(
)+( -
- )+…+(
)+…+( -
- )]=2n+
)]=2n+ -
- <2n+
<2n+ .
.
∴2n<c1+c2+…+cn<2n+ 成立.
成立.
分析:(1)利用 即可求出an;
即可求出an;
(2)利用“错位相减法”即可得出;
(3)利用基本不等式的性质和“裂项求和”即可得出.
点评:熟练掌握公式 、“错位相减法”、基本不等式的性质和“裂项求和”是解题的关键.
、“错位相减法”、基本不等式的性质和“裂项求和”是解题的关键.
∴
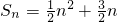 ,
,∴当n=1时,
 ;
;当n≥2时,an=Sn-Sn-1=

 .
.当n=1时,也适合上式,
因此
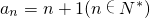 .
.(2)由(1)可得:
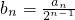 =
= .
.∴Tn=
 ,
, ,
,两式相减得
 =1+
=1+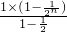
 =3
=3
∴
 .
.(3)证明:由cn=
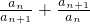 =
= +
+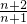 >2
>2 =2,
=2,∴c1+c2+…+cn>2n.
又cn=
 +
+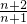 =2+
=2+ -
- ,
,∴c1+c2+…+cn=2n+[(
 -
- )+(
)+( -
- )+…+(
)+…+( -
- )]=2n+
)]=2n+ -
- <2n+
<2n+ .
.∴2n<c1+c2+…+cn<2n+
 成立.
成立.分析:(1)利用
 即可求出an;
即可求出an;(2)利用“错位相减法”即可得出;
(3)利用基本不等式的性质和“裂项求和”即可得出.
点评:熟练掌握公式
 、“错位相减法”、基本不等式的性质和“裂项求和”是解题的关键.
、“错位相减法”、基本不等式的性质和“裂项求和”是解题的关键. 
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|