题目内容
设函数f(x)为R上的奇函数满足f(x+2)=-f(x),且当x∈(0,1)时, ,则
,则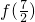 的值为________.
的值为________.
-4
分析:由f(x+2)=-f(x)可求得函数f(x)的周期,利用周期性、奇偶性可把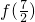 转化到已知区间上求解.
转化到已知区间上求解.
解答:由f(x+2)=-f(x),得f(x+4)=-f(x+2)=-[-f(x)]=f(x),
所以4为f(x)的周期,
则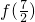 =f(
=f( )=f(-
)=f(- ),
),
又f(x)为R上的奇函数,
所以f( )=-f(
)=-f( )=-
)=- =-4,
=-4,
故答案为:-4.
点评:本题考查函数的周期性、奇偶性及其应用,考查学生灵活运用所学知识分析解决问题的能力.
分析:由f(x+2)=-f(x)可求得函数f(x)的周期,利用周期性、奇偶性可把
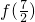 转化到已知区间上求解.
转化到已知区间上求解.解答:由f(x+2)=-f(x),得f(x+4)=-f(x+2)=-[-f(x)]=f(x),
所以4为f(x)的周期,
则
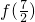 =f(
=f( )=f(-
)=f(- ),
),又f(x)为R上的奇函数,
所以f(
 )=-f(
)=-f( )=-
)=- =-4,
=-4,故答案为:-4.
点评:本题考查函数的周期性、奇偶性及其应用,考查学生灵活运用所学知识分析解决问题的能力.

练习册系列答案
相关题目
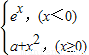 为R上的连续函数,则a等于( )
为R上的连续函数,则a等于( )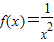 ,则
,则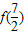 的值为 .
的值为 .