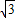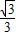Question

已知角α的顶点在原点，始边与x轴的非负半轴重合，终边经过点P（3，y），且tanα=-

4

3

，
（1）求sinα+cosα的值；
（2）求

sin(π-α)+2cos(π+α)

sin( 3 2 π-α)-cos( 3 2 π+α)

的值．

Answer 1

分析：（1）根据P坐标，利用任意角三角函数定义表示出tanα，将已知tanα的值代入求出y的值，确定出P到原点的距离r，再利用任意角的三角函数定义求出sinα与cosα的值，即可确定出sinα+cosα的值；
（2）原式利用诱导公式化简，再利用同角三角函数间的基本关系变形，将tanα的值代入计算即可求出值．

解答：解：（1）∵角α的顶点在原点，始边与x轴的非负半轴重合，终边经过点P（3，y），tanα=

y

3

=-

4

3

，
∴y=-4，
∴r=

x2+y2

=5，
∴sinα=-

4

5

，cosα=

3

5

，
则sinα+cosα=-

1

5

；
（2）∵sinα=-

4

5

，cosα=

3

5

，
∴tanα=-

4

3

，
则原式=

sinα-2cosα

-cosα-sinα

=

tanα-2

-1-tanα

=

- 4 3 -2

-1+ 4 3

=

- 10 3

1 3

=-10．

点评：此题考查了运用诱导公式化简求值，以及任意角的三角函数定义，熟练掌握诱导公式是解本题的关键．