题目内容
(1)
写出从a，b，c，d这4个字母中，每次取出2个字母的所有排列；(2)
写出从a，b，c，d这4个字母中，每次取出3个字母的所有排列．
答案：略
解析：
解析：
|
解析： (1)把a，b，c，d中的任意一个字母排在第一个位置上，有4种排法；第一个位置上的字母排好后，第二个位置上的字母就有3种排法．若第一个位置是 a，那么第二个位置可以是b，c或d，有3个排列，即ab，ac，ad．同理，第一个位置更换为 b，c或d，也分别各有3个排列，如图所示．
因此，共计有 12个不同的排列；它们是ab，ac，ad，ba，bc，bd，ca，cb，cd，da，db，dc．(2) 根据(1)，从4个字母中每次取出2个字母的排列有12种，在每一种这样的排列后面排上其余两个字母中的任一个，就得到取出3个字母的所有排列．可以画出树形图如图所示．
因此，共计有 24个不同的排列，它们是abc，abd，acb，acd，adb，adc，bac，bad，bca，bcd，bda，bdc，cab，cad，cba，cbd，cda，cdb，dab，dac，dba，dbc，bca，dcb． |
练习册系列答案
相关题目
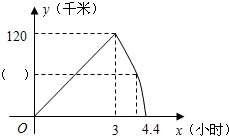甲、乙两车同时从A地出发，以各自的速度匀速向B地行驶．甲车先到达B地，停留1小时后按原路以另一速度匀速返回，直到两车相遇．乙车的速度为每小时60千米．下图是两车之间的距离y（千米）与乙车行驶时间x（小时）之间的函数图象．
