Question

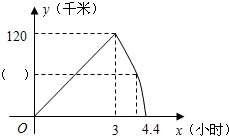甲、乙两车同时从A地出发，以各自的速度匀速向B地行驶．甲车先到达B地，停留1小时后按原路以另一速度匀速返回，直到两车相遇．乙车的速度为每小时60千米．下图是两车之间的距离y（千米）与乙车行驶时间x（小时）之间的函数图象．
（1）请将图中的

60

内填上正确的值，并直接写出甲车从A到B的行驶速度；
（2）求从甲车返回到与乙车相遇过程中y与x之间的函数关系式，并写出自变量x的取值范围．
（3）求出甲车返回时行驶速度及A、B两地的距离．

Answer 1

分析：（1）由图可知，在x=3小时，A、B相距120千米，由此可求甲车从A到B的行驶速度；
（2）由已知，x=4时甲返回，可得坐标（4，60），设出x∈[4，4.4]时，函数的解析式，代入点的坐标，即可求y与x之间的函数关系式；
（3）由图中数据可求甲车返回时行驶速度；A、B两地相距．

解答：解：（1）由图可知，在x=3小时，A、B相距120千米
则甲车的速度为

120

3

+60=100千米/小时；
（2）由已知，x=4时甲返回，则M坐标为（4，60）
设x∈[4，4.4]时，y=kx+b
将（4，60），（4.4，0）代入得

4.4k+b=0 4k+b=60

．
解得

k=-150 b=660

甲车返回到与乙车相遇过程中y=-150x+660，x∈[4，4.4]；
（3）甲车返回时行驶速度为150-60=90千米/小时；A、B两地相距100×3=300千米．

点评：本题考查利用数学知识解决实际问题，考查学生分析解决问题的能力，属于基础题．