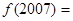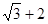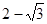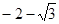题目内容
(本小题满分12分)
已知定义在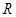 上的函数
上的函数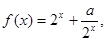
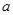 为常数,若
为常数,若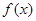 为偶函数,
为偶函数,
(1)求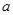 的值;
的值;
(2)判断函数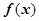 在
在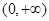 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;
(3)求函数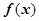 的值域.
的值域.
已知定义在
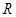 上的函数
上的函数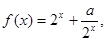
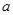 为常数,若
为常数,若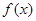 为偶函数,
为偶函数,(1)求
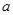 的值;
的值;(2)判断函数
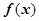 在
在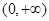 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;(3)求函数
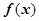 的值域.
的值域.(1) ;(2)定义法证明
;(2)定义法证明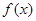 在
在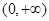 上单调增;(3)函数的值域为
上单调增;(3)函数的值域为 。
。
 ;(2)定义法证明
;(2)定义法证明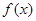 在
在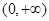 上单调增;(3)函数的值域为
上单调增;(3)函数的值域为 。
。试题分析:(1)由
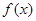 为偶函数,
为偶函数,得
 ,
,从而
 ;
; 
(2)
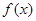 在
在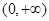 上单调增
上单调增证明:任取
 且
且 ,
, 
 ,
,当
 ,且
,且 ,
, ,
,
从而
 ,即
,即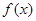 在
在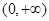 上单调增;
上单调增;(3)函数

令
 ,则
,则 

函数在
 递减,在
递减,在 递增.(这里要简要的证明一下,假如没有证明扣1分)..14分
递增.(这里要简要的证明一下,假如没有证明扣1分)..14分所以函数的值域为
 …
…点评:典型题,研究函数的奇偶性、单调性,是高一阶段研究的主要函数性质,往往以具体函数为载体,综合考查学生灵活运用知识的能力。本题中(3)小题得到
 后,利用换元思想,转化成“对号函数”的研究,值得注意。
后,利用换元思想,转化成“对号函数”的研究,值得注意。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
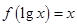 ,则
,则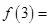 ( )
( )


 ,若
,若 ,则
,则 =( )
=( )



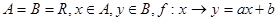 是从
是从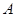 到
到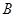 的映射,若1和8的原象分别是3和10,则5在
的映射,若1和8的原象分别是3和10,则5在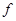 下的象是( )
下的象是( )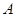 和
和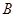 的含铁率
的含铁率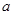 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的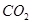 的排放量
的排放量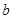 及每万吨铁矿石的价格
及每万吨铁矿石的价格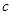 如下表:
如下表: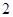 (万吨),则购买铁矿石的最少费用为
(万吨),则购买铁矿石的最少费用为 (百万元).
(百万元).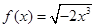 与
与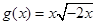 ; ②
; ②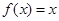 与
与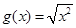 ;
;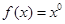 与
与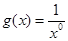 ; ④
; ④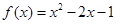 与
与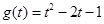 。
。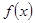 的定义域为实数集R,
的定义域为实数集R,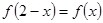 ,且当
,且当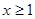 时,
时,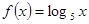 ,则有( )
,则有( )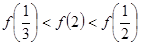
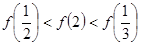
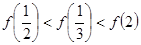
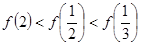
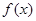 是定义在R上的函数且
是定义在R上的函数且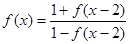 ,且
,且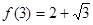 ,则
,则