题目内容
△ABC中,求证:sinA+sinB+sinC≤cos| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
分析:先把sinA+sinB+sinC两两结合,利用和差化积公式化简整理,利用三角形内角和进行转化,最后利用cos
≤1,cos
≤1,cos
≤0,证明出原式.
| A-B |
| 2 |
| A-C |
| 2 |
| B-C |
| 2 |
解答:解:sinA+sinB+sinC=
[(sinA+sinB)+(sinA+sinC)+(sinB+sinC)]
=
(2sin
cos
+2sin
cos
+2sin
cos
)
=cos
cos
+cos
cos
+cos
cos
≤cos
+cos
+cos
原式得证.
| 1 |
| 2 |
=
| 1 |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+C |
| 2 |
| A-C |
| 2 |
| B+C |
| 2 |
| B-C |
| 2 |
=cos
| C |
| 2 |
| A-B |
| 2 |
| B |
| 2 |
| A-C |
| 2 |
| A |
| 2 |
| B-C |
| 2 |
| A |
| 2 |
| B |
| 2 |
| C |
| 2 |
原式得证.
点评:本题主要考查了两用和差化积对三角函数化简求值.三角函数中基础公式较多,平时应注意多积累.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
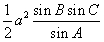 ;
;