题目内容
(1)证明三角形的面积公式S=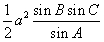 ;
;
(2)在△ABC中,求证:c(acosB-bcosA)=a2-b2。
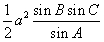 ;
;(2)在△ABC中,求证:c(acosB-bcosA)=a2-b2。
证明:(1)S= ,
,
又 ,
,
∴b= ,
,
∴S= ;
;
(2)左边=c
 =右边。
=右边。
 ,
,又
 ,
,∴b=
 ,
, ∴S=
 ;
; (2)左边=c

 =右边。
=右边。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
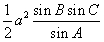 ;
; ,
, ,
, ,
,  ;
; 
 =右边。
=右边。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案