Question

【题目】已知矩阵.

（1）求直线在对应的变换作用下所得的曲线方程；

（2）求矩阵的特征值与特征向量.

Answer 1

【答案】（1）；（2）属于特征值的一个特征向量为，属于特征值的一个特征向量为.

【解析】

（1）设是直线上任一点，在变换作用下变为，利用矩阵变换关系，将用表示，代入，即可求解；

（2）由特征多项式求出特征值，进而求出对应的特征向量.

（1）设是直线上任一点，

在矩阵变换作用下变为，则，

，，，

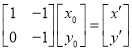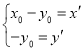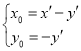，即，

所以变换后的曲线方程为；

（2）矩阵的特征多项式为，

令，得或，

当时，对应的特征向量应满足，

得，所以对应的一个特征向量为，

当时，对应的特征向量应满足，

，得，所以对应的一个特征向量为，

矩阵属于特征值的一个特征向量为，

属于特征值的一个特征向量为.