题目内容
已知f(x)=sinx cosx+sin2x.
cosx+sin2x.
(1)求f(x)的最小正周期和单调递增区间;
(2)若f(x)的图象关于直线x=x0对称,且﹣1<x0<0,求x0的值.
 cosx+sin2x.
cosx+sin2x.(1)求f(x)的最小正周期和单调递增区间;
(2)若f(x)的图象关于直线x=x0对称,且﹣1<x0<0,求x0的值.
解:f(x)=sinxcosx+sin2x= sin2x+
sin2x+ =
=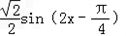
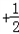
(1)∴最小正周期为T=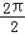 =π,
=π,
由2k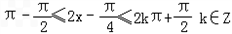 ,
,
得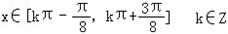 ,
,
∴f(x)的单调增区间是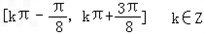 .
.
(2)由题意: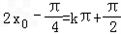 ,得
,得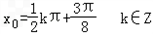 ,
,
∵﹣1<x0<0,即 ,
,
当k=﹣1时,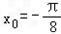 .
.
 sin2x+
sin2x+ =
=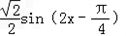
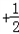
(1)∴最小正周期为T=
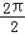 =π,
=π,由2k
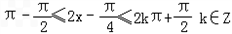 ,
,得
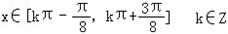 ,
,∴f(x)的单调增区间是
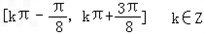 .
.(2)由题意:
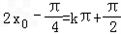 ,得
,得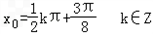 ,
,∵﹣1<x0<0,即
 ,
,当k=﹣1时,
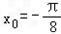 .
.
练习册系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| A、与g(x)的图象相同 | ||
| B、与g(x)的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|