题目内容
若0<t≤ ,则
,则 -t的最小值是( )
-t的最小值是( )A.-2
B.
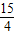
C.2
D.0
【答案】分析:根据“减”-“增”=“减”的原则,判断函数y= -t在区间(0,
-t在区间(0, ]上的单调性,进而可得最值
]上的单调性,进而可得最值
解答:解:令y= -t,
-t,
根据“减”-“增”=“减”的原则
可知:函数y= -t在区间(0,
-t在区间(0, ]上为减函数
]上为减函数
故当x= 时
时 -t的最小值是
-t的最小值是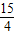
故选B
点评:本题以求最值为载体,考查了函数单调性的性质,熟练掌握函数单调性的性质,并判断出函数的单调性是解答的关键.
 -t在区间(0,
-t在区间(0, ]上的单调性,进而可得最值
]上的单调性,进而可得最值解答:解:令y=
 -t,
-t,根据“减”-“增”=“减”的原则
可知:函数y=
 -t在区间(0,
-t在区间(0, ]上为减函数
]上为减函数故当x=
 时
时 -t的最小值是
-t的最小值是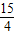
故选B
点评:本题以求最值为载体,考查了函数单调性的性质,熟练掌握函数单调性的性质,并判断出函数的单调性是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2007
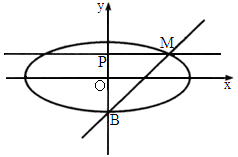
北京崇文模拟)如下图,已知点B是椭圆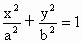 (a>b>0)的短轴位于x轴下方的端点,过B作斜率为l的直线交椭圆于点M,点P在y轴上,且MP∥x轴,
(a>b>0)的短轴位于x轴下方的端点,过B作斜率为l的直线交椭圆于点M,点P在y轴上,且MP∥x轴,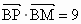 ,若点P的坐标为(0,t),则t的取值范围是
,若点P的坐标为(0,t),则t的取值范围是
[
]|
A .0<t<3 |
B .0<t<b |
|
C .0<t<1 |
D . |
 ,则
,则 -t的最小值是
-t的最小值是