题目内容
设首项不为零的等差数列{an}前n项之和是Sn,若不等式an2+| Sn2 | n2 |
分析:等差数列{an}中,首项不为零,前n项和Sn=
;由不等式an2+
≥λa12,得an2+
≥λa12,整理得
(
)2+
+
≥λ;若设t=
,求函数y=
t2+
t+
的最小值,得λ的最大值.
| n(a1+an) |
| 2 |
| Sn2 |
| n2 |
| ||
| n2 |
| 5 |
| 4 |
| an |
| a1 |
| 1 |
| 2 |
| an |
| a1 |
| 1 |
| 4 |
| an |
| a1 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:在等差数列{an}中,首项不为零,即a1≠0;则数列的前n项之和为Sn=
;
由不等式an2+
≥λa12,得an2+
≥λa12,
∴
an2+
a1an+
a12≥λa12,即
(
)2+
+
≥λ;
设t=
,则y=
t2+
t+
=
(t+
)2+
≥
,
∴λ≤
,即λ的最大值为
;
故答案为
.
| n(a1+an) |
| 2 |
由不等式an2+
| Sn2 |
| n2 |
| ||
| n2 |
∴
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
| an |
| a1 |
| 1 |
| 2 |
| an |
| a1 |
| 1 |
| 4 |
设t=
| an |
| a1 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
∴λ≤
| 1 |
| 5 |
| 1 |
| 5 |
故答案为
| 1 |
| 5 |
点评:本题考查了数列与不等式的综合应用,其中用到换元法求得二次函数的最值,应属于考查计算能力的基础题目.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
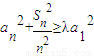 对任意an和正整数n恒成立,则实数λ的最大值为 .
对任意an和正整数n恒成立,则实数λ的最大值为 .