题目内容
平面直角坐标系xOy中,点P(x,y )满足条件:(|x|+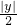 -1 ) (|x|+
-1 ) (|x|+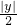 -2 ) (|x|+
-2 ) (|x|+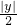 -3 )<0,则点P所在区域的面积为________.
-3 )<0,则点P所在区域的面积为________.
24
分析:当x>0,y>0时,原不等式化为:(x+ -1 ) (x+
-1 ) (x+ -2 ) (x+
-2 ) (x+ -3 )<0解得:
-3 )<0解得:
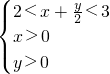 或
或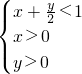 画出不等式组此不等式表示的平面区域:如图所示.其面积为:6.根据对称性可得条件:(|x|+
画出不等式组此不等式表示的平面区域:如图所示.其面积为:6.根据对称性可得条件:(|x|+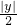 -1 ) (|x|+
-1 ) (|x|+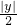 -2 ) (|x|+
-2 ) (|x|+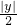 -3 )<0,在另外三个象限内的图象的面积,从而得点P所在区域的面积.
-3 )<0,在另外三个象限内的图象的面积,从而得点P所在区域的面积.
解答: 解:当x>0,y>0时,原不等式化为:
解:当x>0,y>0时,原不等式化为:
(x+ -1 ) (x+
-1 ) (x+ -2 ) (x+
-2 ) (x+ -3 )<0
-3 )<0
设x+ =t,则(t-1)(t-2)(t-3)<0
=t,则(t-1)(t-2)(t-3)<0
即:t<1或2<t<3.
画出不等式组
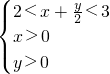 或
或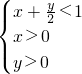 表示的平面区域:如图所示.
表示的平面区域:如图所示.
其面积为:6.
根据对称性可得:
条件:(|x|+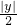 -1 ) (|x|+
-1 ) (|x|+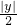 -2 ) (|x|+
-2 ) (|x|+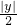 -3 )<0,在另外三个象限内的图象的面积也分别是:6.
-3 )<0,在另外三个象限内的图象的面积也分别是:6.
则点P所在区域的面积为:6×4=24.
故答案为:24.
点评:本题考查了二元一次不等式(组)与平面区域,平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.
分析:当x>0,y>0时,原不等式化为:(x+
 -1 ) (x+
-1 ) (x+ -2 ) (x+
-2 ) (x+ -3 )<0解得:
-3 )<0解得: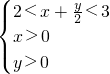 或
或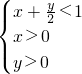 画出不等式组此不等式表示的平面区域:如图所示.其面积为:6.根据对称性可得条件:(|x|+
画出不等式组此不等式表示的平面区域:如图所示.其面积为:6.根据对称性可得条件:(|x|+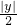 -1 ) (|x|+
-1 ) (|x|+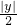 -2 ) (|x|+
-2 ) (|x|+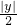 -3 )<0,在另外三个象限内的图象的面积,从而得点P所在区域的面积.
-3 )<0,在另外三个象限内的图象的面积,从而得点P所在区域的面积.解答:
 解:当x>0,y>0时,原不等式化为:
解:当x>0,y>0时,原不等式化为:(x+
 -1 ) (x+
-1 ) (x+ -2 ) (x+
-2 ) (x+ -3 )<0
-3 )<0设x+
 =t,则(t-1)(t-2)(t-3)<0
=t,则(t-1)(t-2)(t-3)<0即:t<1或2<t<3.
画出不等式组
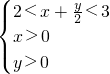 或
或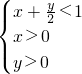 表示的平面区域:如图所示.
表示的平面区域:如图所示.其面积为:6.
根据对称性可得:
条件:(|x|+
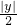 -1 ) (|x|+
-1 ) (|x|+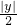 -2 ) (|x|+
-2 ) (|x|+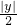 -3 )<0,在另外三个象限内的图象的面积也分别是:6.
-3 )<0,在另外三个象限内的图象的面积也分别是:6.则点P所在区域的面积为:6×4=24.
故答案为:24.
点评:本题考查了二元一次不等式(组)与平面区域,平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
相关题目
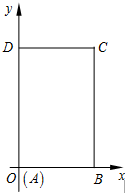 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.