题目内容
已知等差数列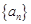 满足:
满足: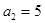 ,
,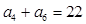 .
.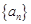 的前n项和为
的前n项和为 .
.
(Ⅰ)求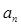 及
及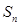 ;
;
(Ⅱ)若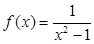 ,
,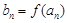 (
(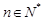 ),求数列
),求数列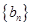 的前
的前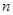 项和
项和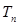 .
.
(Ⅰ)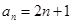 ,
,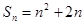 (Ⅱ)
(Ⅱ)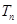 =
=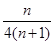
解析试题分析:(Ⅰ)设出首项a1和公差d ,利用等差数列通项公式,就可求出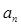 ,再利用等差数列前项求和公式就可求出
,再利用等差数列前项求和公式就可求出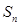 ;(Ⅱ)由(Ⅰ)知
;(Ⅱ)由(Ⅰ)知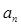 ,再利用
,再利用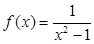 ,
,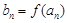 (
(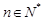 ),就可求出
),就可求出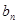 ,再利用错位相减法就可求出
,再利用错位相减法就可求出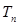 .
.
试题解析:(Ⅰ)设等差数列{an}的首项为a1,公差为d
∵ 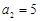 ,
,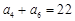 ∴
∴ 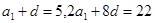 解得
解得 
∴ 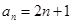
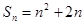 ,
,
(Ⅱ)∵ 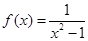 ,
,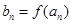 ∴
∴ 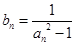
∵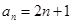 ∴
∴ 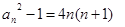
∴ 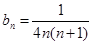
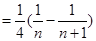
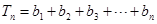
= 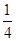 (1-
(1- 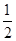 +
+ 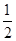 -
- 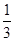 +…+
+…+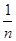 -
- )
)
=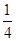 (1-
(1- ) =
) =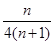
所以数列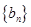 的前
的前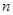 项和
项和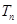 =
=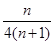 .
.
考点:1.等差数列的通项公式; 2. 等差数列的前n项和公式; 3.裂项法求数列的前n项和公式

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
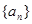 的前
的前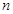 项的和为
项的和为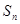 ,
, 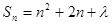 ,求证:数列
,求证:数列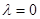 .
.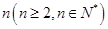 的两个数列
的两个数列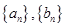 满足
满足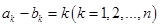 且集合
且集合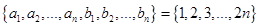 ,则称数列
,则称数列 项相关数列”.
项相关数列”.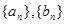 是一对“4项相关数列”,求
是一对“4项相关数列”,求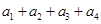 和
和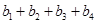 的值,并写出一对“
的值,并写出一对“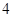 项相
项相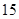 项相关数列”
项相关数列”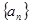 及其前
及其前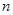 项和
项和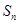 满足:
满足: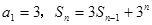 (
(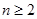 ,
,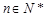 ).
).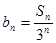 ,
,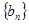 是等差数列;
是等差数列;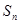 及
及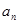 ;
;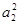 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,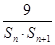 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.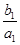 +
+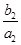 +…+
+…+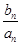 =1-
=1-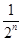 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.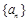 的前n项和为
的前n项和为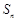 ,且
,且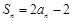 .
.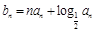 ,数列
,数列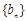 的前n项和为
的前n项和为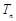 ,若不等式
,若不等式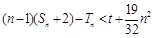 对任意
对任意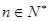 恒成立,求实数
恒成立,求实数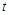 的取值范围.
的取值范围. 中,
中,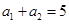 ,
,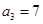 ,记数列
,记数列 的前
的前 项和为
项和为 .
. 、
、 ,使得
,使得 、
、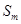 、
、 中
中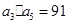 ,
, ,求
,求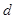 ;
; .
.