题目内容
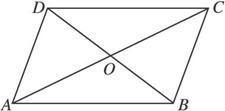
如下图，平行四边形ABCD中，点M是AB的中点，点N在BD上，且BN=
BD，求证：M、N、C三点共线.
思路分析：共线问题，一般情况下可化成向量共线，再利用向量共线的条件证明.
证明：设
=e1，=e2，
∵
=
-
=e2-e1，
=
，
∴
=
e1.∴
=
+
=
e1+e2.
又
=
，∴
=
（e2-e1）.
∴
=
+
=
e1+
（e2-e1）
=
e1+
e2.
∴
=3
.∴M、N、C三点共线.
练习册系列答案
相关题目
BD，求证：M、N、C三点共线.
和
都不共线的向量共有（ ）
+
|=|
-
|，则必有（ ）
=0 B.
=0或
=0 C.ABCD为矩形 D.ABCD为正方形
,
,则下列结论不正确的是( )
时,四边形EFGH是平行四边形
时,四边形EFGH是梯形
.
=a,
=b为边的平行四边形，其中BM=
BC，CN=
CD.试以向量a,b为一组基底,表示出向量
,
.