题目内容
已知中心在原点,焦点在x轴上的椭圆,离心率 ,且经过抛物线x2=4y的焦点.
,且经过抛物线x2=4y的焦点.
(1)求椭圆的标准方程;
(2)若过点B(0,-2)的直线l(斜率不等于零)与椭圆交于不同的两点E,F(E在B,F之间),△OBE与△OBF面积之比为λ,求λ的取值范围.
解:(1)由已知得F(0,1),设椭圆方程为 (a>b>0),则b=1
(a>b>0),则b=1
∵椭圆的离心率为 ,∴
,∴ ,
,
∵a2=b2+c2,∴a2=2,c=1
∴椭圆方程为 +y2=1;
+y2=1;
(2)由题意知l的斜率存在且不为零,设l方程为y=mx-2(m≠0)①,代入 +y2=1,
+y2=1,
整理得(2m2+1)x2-8mx+6=0,由△>0得m2> .
.
设E(x1,y1),F(x2,y2),则x1+x2=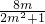 ,x1x2=
,x1x2=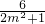 ②
②
∵△OBE与△OBF面积之比为λ
∴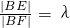 ,∴
,∴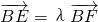
∴x2=λx1.
代入②得,消去x1得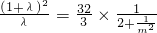 ,
,
∵m2> .
.
∴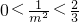
∴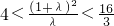
∴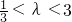 且λ≠1
且λ≠1
分析:(1)设椭圆的标准方程,根据离心率求得a和c的关系,根据经过抛物线x2=4y的焦点求得b,从而可求椭圆的方程;(2)设直线l方程,与椭圆方程联立消去y,根据判别式大于0确定m的范围,将三角形面积之比转化为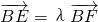 ,进而可得λ,m的关系式,由此即可确定λ的范围.
,进而可得λ,m的关系式,由此即可确定λ的范围.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,解题的关键是联立方程,利用韦达定理进行求解.
 (a>b>0),则b=1
(a>b>0),则b=1∵椭圆的离心率为
 ,∴
,∴ ,
,∵a2=b2+c2,∴a2=2,c=1
∴椭圆方程为
 +y2=1;
+y2=1;(2)由题意知l的斜率存在且不为零,设l方程为y=mx-2(m≠0)①,代入
 +y2=1,
+y2=1,整理得(2m2+1)x2-8mx+6=0,由△>0得m2>
 .
.设E(x1,y1),F(x2,y2),则x1+x2=
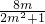 ,x1x2=
,x1x2=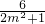 ②
②∵△OBE与△OBF面积之比为λ
∴
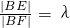 ,∴
,∴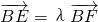
∴x2=λx1.
代入②得,消去x1得
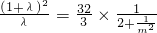 ,
,∵m2>
 .
.∴
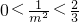
∴
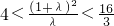
∴
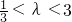 且λ≠1
且λ≠1分析:(1)设椭圆的标准方程,根据离心率求得a和c的关系,根据经过抛物线x2=4y的焦点求得b,从而可求椭圆的方程;(2)设直线l方程,与椭圆方程联立消去y,根据判别式大于0确定m的范围,将三角形面积之比转化为
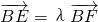 ,进而可得λ,m的关系式,由此即可确定λ的范围.
,进而可得λ,m的关系式,由此即可确定λ的范围.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,解题的关键是联立方程,利用韦达定理进行求解.

练习册系列答案
相关题目