题目内容
在直角坐标系xOy中,直线l与x轴正半轴和y轴正半轴分别相交于A,B两点,△AOB的内切圆为⊙M.
(1)如果⊙M半径为1,l与⊙M切于点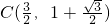 ,求直线l的方程;
,求直线l的方程;
(2)如果⊙M半径为1,证明当△AOB的面积、周长最小时,此时△AOB为同一三角形;
(3)如果l的方程为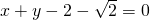 ,P为⊙M上任一点,求PA2+PB2+PO2的最值.
,P为⊙M上任一点,求PA2+PB2+PO2的最值.
解:(1)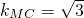 ,(1分),
,(1分),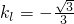 .
.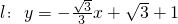 .
.
(2)设A(a,0),B(0,b),(a>2,b>2),
l:bx+ay-ab=0.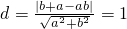 ,
,
(a-2)(b-2)=2,ab-2(a+b)+2=0,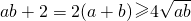 ,
,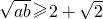 ,(6分)
,(6分)
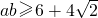 .当且仅当
.当且仅当 时,
时,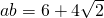 .
.
面积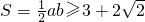 ,
,
此时△AOB为直角边长为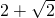 的等腰直角三角形.
的等腰直角三角形.
周长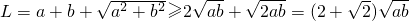
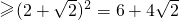 .
.
此时△AOB为直角边长为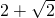 的等腰直角三角形.
的等腰直角三角形.
∴此时的△AOB为同一三角形.
(3)l的方程为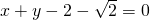 ,得
,得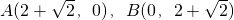 ,
,
⊙M:(x-1)2+(y-1)2=1,设P(m,n)为圆上任一点,
则:(m-1)2+(n-1)2=1,m2+n2=2(m+n)-1,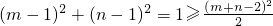 ,
,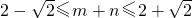 .
.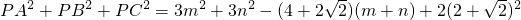 =
=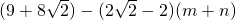 .
.
当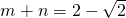 时,
时,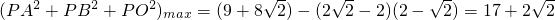 .
.
此时,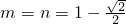 .
.
当 时,
时,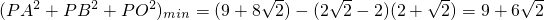 .
.
此时,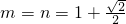 .
.
分析:(1)先求得圆心与切点连线的斜率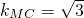 再由两者互为负倒数求得
再由两者互为负倒数求得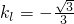 .进而求得直线l的方程;
.进而求得直线l的方程;
(2)设A(a,0),B(0,b),(a>2,b>2),直线AB的方程为::bx+ay-ab=0.圆心到该直线的距离为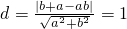 ,整理得(a-2)(b-2)=2,有ab-2(a+b)+2=0,再由基本不等式得
,整理得(a-2)(b-2)=2,有ab-2(a+b)+2=0,再由基本不等式得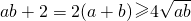 ,
,
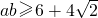 .三角形面积
.三角形面积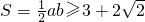 ,周长
,周长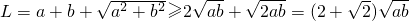
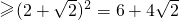 .取得最值的条件一致.所以△AOB为同一三角形.
.取得最值的条件一致.所以△AOB为同一三角形.
(3)l的方程为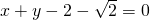 ,解得
,解得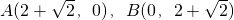 ,P(m,n)为圆上任一点,
,P(m,n)为圆上任一点,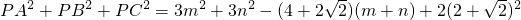 =
=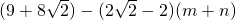 .
.
又因为(m-1)2+(n-1)2=1,m2+n2=2(m+n)-1,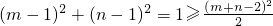 ,所以
,所以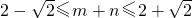 代入上式求解即可.
代入上式求解即可.
点评:本题主要考查直线与圆的位置关系及其方程的应用,还考查了用解析法研究三角形面积,周长及线段长的最值问题,
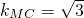 ,(1分),
,(1分),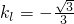 .
.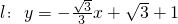 .
.(2)设A(a,0),B(0,b),(a>2,b>2),
l:bx+ay-ab=0.
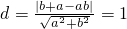 ,
,(a-2)(b-2)=2,ab-2(a+b)+2=0,
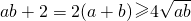 ,
,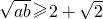 ,(6分)
,(6分)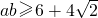 .当且仅当
.当且仅当 时,
时,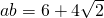 .
.面积
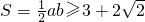 ,
,此时△AOB为直角边长为
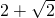 的等腰直角三角形.
的等腰直角三角形.周长
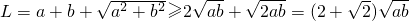
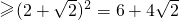 .
.此时△AOB为直角边长为
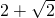 的等腰直角三角形.
的等腰直角三角形.∴此时的△AOB为同一三角形.
(3)l的方程为
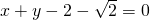 ,得
,得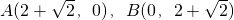 ,
,⊙M:(x-1)2+(y-1)2=1,设P(m,n)为圆上任一点,
则:(m-1)2+(n-1)2=1,m2+n2=2(m+n)-1,
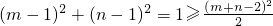 ,
,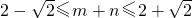 .
.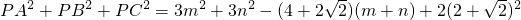 =
=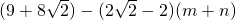 .
.当
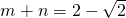 时,
时,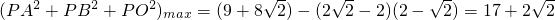 .
.此时,
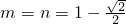 .
.当
 时,
时,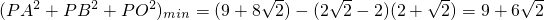 .
.此时,
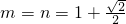 .
.分析:(1)先求得圆心与切点连线的斜率
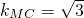 再由两者互为负倒数求得
再由两者互为负倒数求得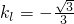 .进而求得直线l的方程;
.进而求得直线l的方程;(2)设A(a,0),B(0,b),(a>2,b>2),直线AB的方程为::bx+ay-ab=0.圆心到该直线的距离为
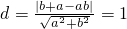 ,整理得(a-2)(b-2)=2,有ab-2(a+b)+2=0,再由基本不等式得
,整理得(a-2)(b-2)=2,有ab-2(a+b)+2=0,再由基本不等式得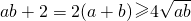 ,
,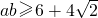 .三角形面积
.三角形面积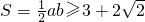 ,周长
,周长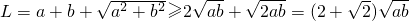
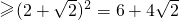 .取得最值的条件一致.所以△AOB为同一三角形.
.取得最值的条件一致.所以△AOB为同一三角形.(3)l的方程为
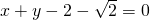 ,解得
,解得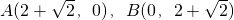 ,P(m,n)为圆上任一点,
,P(m,n)为圆上任一点,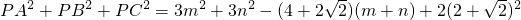 =
=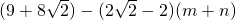 .
.又因为(m-1)2+(n-1)2=1,m2+n2=2(m+n)-1,
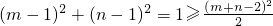 ,所以
,所以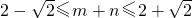 代入上式求解即可.
代入上式求解即可.点评:本题主要考查直线与圆的位置关系及其方程的应用,还考查了用解析法研究三角形面积,周长及线段长的最值问题,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为