题目内容
(本小题满分12分)
设p,q为实数,α,β是方程 的两个实根,数列
的两个实根,数列 满足
满足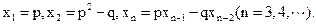
(1)证明:
(2)求数列 的通项公式;
的通项公式;
(3)若 求
求 的前n项和
的前n项和 。
。
设p,q为实数,α,β是方程
 的两个实根,数列
的两个实根,数列 满足
满足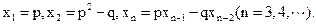
(1)证明:

(2)求数列
 的通项公式;
的通项公式;(3)若
 求
求 的前n项和
的前n项和 。
。(1)证明见解析。
(2)
(3)
(2)

(3)

本题(1)容易证明,本题(2)是一个典型的递归数列求通项问题,此类问题的常用方法是构造等比数列求解,利用此法可求得{xn}的通项公式;而(3)是一个典型的错位相减法,计算时要格外细心,此类问题主要就是考查学生的运算能力。
(1)根据求根公式得方程 的根为
的根为
 ;
;
(2) ,
, ,即数列
,即数列 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
由 有
有

当 即
即 时,
时, ,
,
当 即
即 时,
时, ,
,
(3)当 时
时 ,此时
,此时 ,
,


 。
。
(1)根据求根公式得方程
 的根为
的根为
 ;
;(2)
 ,
, ,即数列
,即数列 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
由
 有
有
当
 即
即 时,
时, ,
,当
 即
即 时,
时, ,
,(3)当
 时
时 ,此时
,此时 ,
,

 。
。
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
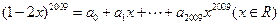 ,则
,则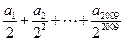 的值为( )
的值为( )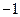
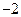
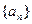
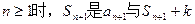
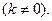
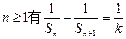 ;
;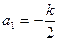 ,求Sn;
,求Sn;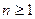 ,试证明:S1S2+S2S3+……+SnS
,试证明:S1S2+S2S3+……+SnS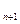
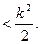
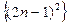 的前
的前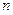 项和
项和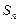 .
. 前n项的和为( )
前n项的和为( )



 是等差数列,且
是等差数列,且
 ,求
,求 的前项的和
的前项的和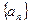 ,
,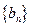 都是等差数列,其中
都是等差数列,其中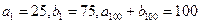 ,那么数列
,那么数列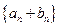 的前
的前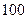 项的和是( ).
项的和是( ).


 中,
中, 项,若
项,若 。
。