题目内容
对任意实数a(a≠0)和b，不等式|a+b|+|a-b|≥|a|(|x-1|+|x-2|)恒成立，试求实数x的取值范围.
所求的x的取值范围是
依题意，|x-1|+|x-2|≤
恒成立，
故|x-1|+|x-2|≤
.
因为|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,
当且仅当(a+b)(a-b)≥0时取“=”，
所以=2.
所以x的取值范围即为不等式|x-1|+|x-2|≤2的解.
解上述不等式得
≤x≤
，
所以所求的x的取值范围是.
恒成立，故|x-1|+|x-2|≤
.因为|a+b|+|a-b|≥|(a+b)+(a-b)|=2|a|,
当且仅当(a+b)(a-b)≥0时取“=”，
所以
=2.所以x的取值范围即为不等式|x-1|+|x-2|≤2的解.
解上述不等式得
≤x≤，所以所求的x的取值范围是
.
练习册系列答案
相关题目
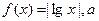、b是满足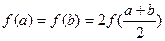
的实数，其中
.
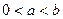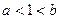；（2）求证：
.
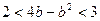的不等式
的解集依次为
与
，求使
的
的取值范围。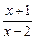
|=
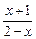的解集是__________.
，使得不等式
成立
，则实数t的取值范围为_____________
，若
，则实数
的取值范围是（ ）
的解集是 ．
的取值范围是 ．