题目内容
9.扇形周长为4,当扇形面积最大时,其圆心角的弧度数为2.分析 设出弧长和半径,由周长得到弧长和半径的关系,再把弧长和半径的关系代入扇形的面积公式,转化为关于半径的二次函数,配方求出面积的最大值.
解答 解:设扇形的半径为r,弧长为l,则l+2r=4,
即l=4-2r(0<r<2),①
扇形的面积S=$\frac{1}{2}$lr,将①代入,得S=$\frac{1}{2}$(4-2r)r=-r2+2r=-(r-1)2+1,
所以当且仅当r=1时,S有最大值1.
此时l=4-2×1=2,α=$\frac{l}{r}$=2.所以当α=2rad时,扇形的面积取最大值.
故答案为:2.
点评 本题考查角的弧度数与度数间的转化,扇形的弧长公式和面积公式的应用,体现了转化的数学思想.

练习册系列答案
相关题目
19.圆C:(x+2)2+y2=32与抛物线y2=2px(p>0)相交于A、B两点,若直线AB恰好经过抛物线的焦点,则p等于( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | 4 |
4. 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )
 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )| A. | 6 | B. | 4.6 | C. | 1.9 | D. | -3.9 |
1.执行如图所示的程序框图,则输出S的值是( )
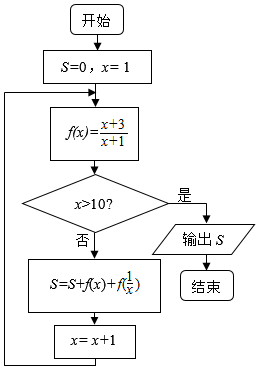

| A. | 36 | B. | 40 | C. | 44 | D. | 48 |
18.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4,则P=( )
| A. | 1 | B. | 4 | C. | 2 | D. | 8 |
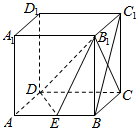 如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,
如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,