题目内容
等差数列{ an}中a3=7,a1+a2+a3=12,记Sn为{an}的前n项和,令bn=anan+1,数列{
}的前n项和为Tn.
(1)求an和Sn;
(2)求证:Tn<
;
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
| 1 |
| bn |
(1)求an和Sn;
(2)求证:Tn<
| 1 |
| 3 |
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
(1)设数列{an}的公差为d,
由a3=a1+2d=7,a1+a2+a3=3a1+3d=12,
解得a1=1,d=3,
∴an=3n-2,
Sn=n+
×3=
.
(2)∵bn=anan+1=(3n-2)(3n+1),
∴
=
=
(
-
),
Tn=
(1-
+
-
+
-
+…+
-
+
-
)
=
(1-
)<
.
(3)由(2)知,Tn=
,∴T1=
,Tm=
,Tn=
,
∵T1,Tm,Tn成等比数列,
∴(
)2=
×
,
即
=
,
当m=1时,7=
,n=1,不合题意;
当m=2时,
=
,n=16,符合题意;
当m=3时,
=
,n无正整数解;
当m=4时,
=
,n无正整数解;
当m=5时,
=
,n无正整数解;
当m=6时,
=
,n无正整数解;
当m≥7时,m2-6m-1=(m-3)2-10>0,
则
<1,而
=3+
>3,
所以,此时不存在正整数m,n,且7<m<n,使得T1,Tm,Tn成等比数列.
综上,存在正整数m=2,n=16,且1<m<n,使得T1,Tm,Tn成等比数列.
由a3=a1+2d=7,a1+a2+a3=3a1+3d=12,
解得a1=1,d=3,
∴an=3n-2,
Sn=n+
| n(n-1) |
| 2 |
| 3n2-n |
| 2 |
(2)∵bn=anan+1=(3n-2)(3n+1),
∴
| 1 |
| bn |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
Tn=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 11 |
| 1 |
| 3n-5 |
| 1 |
| 3n-2 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
=
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
(3)由(2)知,Tn=
| n |
| 3n+1 |
| 1 |
| 4 |
| m |
| 3m+1 |
| n |
| 3n+1 |
∵T1,Tm,Tn成等比数列,
∴(
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
即
| 6m+1 |
| m2 |
| 3n+4 |
| n |
当m=1时,7=
| 3n+4 |
| n |
当m=2时,
| 13 |
| 4 |
| 3n+4 |
| n |
当m=3时,
| 19 |
| 9 |
| 3n+4 |
| n |
当m=4时,
| 25 |
| 16 |
| 3n+4 |
| n |
当m=5时,
| 31 |
| 25 |
| 3n+4 |
| n |
当m=6时,
| 37 |
| 36 |
| 3n+4 |
| n |
当m≥7时,m2-6m-1=(m-3)2-10>0,
则
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 4 |
| n |
所以,此时不存在正整数m,n,且7<m<n,使得T1,Tm,Tn成等比数列.
综上,存在正整数m=2,n=16,且1<m<n,使得T1,Tm,Tn成等比数列.

练习册系列答案
相关题目
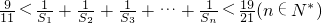 的所有n值的和为________.
的所有n值的和为________.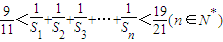 的所有n值的和为 .
的所有n值的和为 .