题目内容
如图,椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 和
和![]() 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
(1)求椭圆M的标准方程;

(2)设直线![]() 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点![]() 直线
直线![]() 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点![]() 求
求![]() 的最大值及取得最大值时
的最大值及取得最大值时![]() 的值.
的值.
解:(1)![]() ……①
……①
矩形ABCD面积为8,即![]() ……②
……②
由①②解得:![]() ,∴椭圆M的标准方程是
,∴椭圆M的标准方程是![]() . ………………4分
. ………………4分
(2)由![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() 得
得![]() .
.
![]() . ………………6分
. ………………6分
线段CD的方程为![]() ,线段AD的方程为
,线段AD的方程为![]() 。
。
①不妨设点S在AB边上,T在CD边上,此时![]() ,
,
因此![]() ,此时
,此时 ,
,
当![]() 时
时![]() 取得最大值
取得最大值![]() ; ………………8分
; ………………8分
②不妨设点S在AD边上,T在CD边上,可知![]() .
.
所以![]() ,则
,则 ,
,
令![]() ,则
,则![]()
所以 ,
,
当且仅当![]()
![]() 时
时![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ; ………………12分
; ………………12分
③不妨设点S在AB边上,T在BC边上,可知![]() ,
,
由椭圆和矩形的对称性可知当![]() 时
时![]() 取得最大值
取得最大值![]() ;
;
综上所述,当![]() 和0时,
和0时,![]() 取得最大值
取得最大值![]() ………………14分
………………14分

练习册系列答案
相关题目




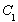














 的离心率为
的离心率为 ,
, 是其左右顶点,
是其左右顶点, 是椭圆上位于
是椭圆上位于 轴两侧的点(点
轴两侧的点(点 在
在 面积的最大值为4.
面积的最大值为4.
 的斜率分别为
的斜率分别为 ,若
,若 ,设△
,设△ 与△
与△ 的面积分别为
的面积分别为 ,求
,求 的最大值.
的最大值. 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为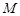 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 ,直线
,直线 分别与
分别与 。
。
 。
。 的面积分别为
的面积分别为 ,若
,若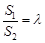 ,求
,求 的取值范围。
的取值范围。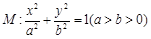 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值. 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.