题目内容
如图,椭圆 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于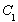 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 相交于点
相交于点 ,直线
,直线 分别与
分别与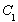 相交于点
相交于点 。
。

(1)求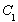 、
、 的方程;
的方程;
(2)求证: 。
。
(3)记 的面积分别为
的面积分别为 ,若
,若 ,求
,求 的取值范围。
的取值范围。
【答案】
(1)
 ;(2)见解析;(3)
;(2)见解析;(3) .
.
【解析】
试题分析:(1)利用椭圆的几何性质,建立 的方程组即得;
的方程组即得;
(2)通过设直线 并联立
并联立 应用韦达定理及平面向量的坐标运算证得
应用韦达定理及平面向量的坐标运算证得 ,从而得到
,从而得到 ;
;
(3)通过设直线 ,联立方程组
,联立方程组 ,
, ;
;
联立 ,
,
利用三角形面积公式分别计算 ,用
,用 表示,从而得到
表示,从而得到 .
.
试题解析:
(1) (1分)
(1分)
又 ,得
,得
 (2分)
(2分)
(2)设直线 则
则 (3分)
(3分)
 =0
=0
 (5分)
(5分)
(3)设直线
 ,同理可得
,同理可得
 (8分)
(8分)

同理可得
 (2分)
(2分)
 (13分)
(13分)
考点:椭圆的几何性质,直线与圆锥曲线的位置关系,韦达定理,平面向量的数量积,基本不等式.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,
, 是其左右顶点,
是其左右顶点, 是椭圆上位于
是椭圆上位于 轴两侧的点(点
轴两侧的点(点 在
在 面积的最大值为4.
面积的最大值为4.
 的斜率分别为
的斜率分别为 ,若
,若 ,设△
,设△ 与△
与△ 的面积分别为
的面积分别为 ,求
,求 的最大值.
的最大值. 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为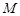 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 ,直线
,直线 分别与
分别与 。
。
 。
。 的面积分别为
的面积分别为 ,若
,若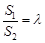 ,求
,求 的取值范围。
的取值范围。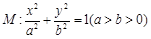 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值. 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.