题目内容
(理)设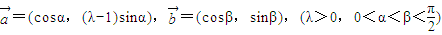 是平面上的两个向量,若向量
是平面上的两个向量,若向量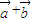 与
与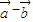 相互垂直,
相互垂直,(1)求实数λ的值;
(2)若
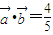 ,且
,且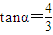 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)
【答案】分析:(1)由题意及平面向量的数量积运算法则进行化简,由α的范围,得到sinα不为0,再由λ大于0,根据化简后的关系式即可求出λ的值;
(2)把第一问求出的λ的值代入 的坐标确定出此向量,然后利用平面向量的数量积运算法则化简
的坐标确定出此向量,然后利用平面向量的数量积运算法则化简 ,可得出cos(α-β)的值,由α与β的范围得出α-β的范围,利用同角三角函数间的基本关系求出sin(α-β)及tan(α-β)的值,再由α=(α-β)+β,利用两角和与差的正切函数公式化简后,将各自的值代入求出tanα的值,即可得出α的度数.
,可得出cos(α-β)的值,由α与β的范围得出α-β的范围,利用同角三角函数间的基本关系求出sin(α-β)及tan(α-β)的值,再由α=(α-β)+β,利用两角和与差的正切函数公式化简后,将各自的值代入求出tanα的值,即可得出α的度数.
解答:解:(1)由题设,得 ,
,
即 ,
,
所以,(λ-1)2sin2α-sin2α=0,
即λ(λ-2)sin2α=0
因为 ,
,
∴sin2α≠0,又λ>0,
所以λ-2=0,即λ=2;
(2)由(1)知, ,
,
∴ ,
,
又 ,
,
∴ ,
,
∵ ,则
,则 ,
,
∴ ,
,
∴ ,
,
又 ,
,
∴ .
.
点评:此题考查了平面向量数量积的运算,利用数量积判断两向量的垂直关系,两角和与差的余弦、正切函数公式,以及同角三角函数间的基本关系,学生做题时特别注意角度的范围及灵活变换.
(2)把第一问求出的λ的值代入
 的坐标确定出此向量,然后利用平面向量的数量积运算法则化简
的坐标确定出此向量,然后利用平面向量的数量积运算法则化简 ,可得出cos(α-β)的值,由α与β的范围得出α-β的范围,利用同角三角函数间的基本关系求出sin(α-β)及tan(α-β)的值,再由α=(α-β)+β,利用两角和与差的正切函数公式化简后,将各自的值代入求出tanα的值,即可得出α的度数.
,可得出cos(α-β)的值,由α与β的范围得出α-β的范围,利用同角三角函数间的基本关系求出sin(α-β)及tan(α-β)的值,再由α=(α-β)+β,利用两角和与差的正切函数公式化简后,将各自的值代入求出tanα的值,即可得出α的度数.解答:解:(1)由题设,得
 ,
,即
 ,
,所以,(λ-1)2sin2α-sin2α=0,
即λ(λ-2)sin2α=0
因为
 ,
,∴sin2α≠0,又λ>0,
所以λ-2=0,即λ=2;
(2)由(1)知,
 ,
,∴
 ,
,又
 ,
,∴
 ,
,∵
 ,则
,则 ,
,∴
 ,
,∴
 ,
,又
 ,
,∴
 .
.点评:此题考查了平面向量数量积的运算,利用数量积判断两向量的垂直关系,两角和与差的余弦、正切函数公式,以及同角三角函数间的基本关系,学生做题时特别注意角度的范围及灵活变换.

练习册系列答案
相关题目
 是平面上的两个向量,若向量
是平面上的两个向量,若向量 与
与 相互垂直,
相互垂直, ,且
,且 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)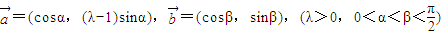 是平面上的两个向量,若向量
是平面上的两个向量,若向量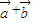 与
与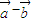 相互垂直,
相互垂直,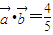 ,且
,且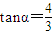 ,求α的值(结果用反三角函数值表示)
,求α的值(结果用反三角函数值表示)