题目内容
判断函数y=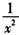 的单调区间。
的单调区间。
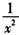 的单调区间。
的单调区间。解:首先对复合函数y= 进行分解(分解为简单函数),
进行分解(分解为简单函数),
设t=x2(t>0),则y= ,然后对简单函数的单调性进行考察,进而得到y=
,然后对简单函数的单调性进行考察,进而得到y= 的单调性,
的单调性,
令t=x2(t>0),∵ 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,
而t=x2在(-∞,0)上为减函数,在(0,+∞)上是增函数,
∴y= 在(-∞,0)上为增函数,在(0,+∞)上为减函数.
在(-∞,0)上为增函数,在(0,+∞)上为减函数.
 进行分解(分解为简单函数),
进行分解(分解为简单函数),设t=x2(t>0),则y=
 ,然后对简单函数的单调性进行考察,进而得到y=
,然后对简单函数的单调性进行考察,进而得到y= 的单调性,
的单调性,令t=x2(t>0),∵
 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,而t=x2在(-∞,0)上为减函数,在(0,+∞)上是增函数,
∴y=
 在(-∞,0)上为增函数,在(0,+∞)上为减函数.
在(-∞,0)上为增函数,在(0,+∞)上为减函数. 
练习册系列答案
相关题目
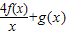 的单调递增区间;
的单调递增区间;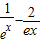 (其中e=2.718…)是否有实数解?并说明理由.
(其中e=2.718…)是否有实数解?并说明理由.