题目内容
椭圆![]() 过点P
过点P![]() ,且离心率为
,且离心率为![]() ,F为椭圆的右焦点,
,F为椭圆的右焦点,![]() 、
、![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且 ![]() ,定点
,定点![]() (-4,0).
(-4,0).
(Ⅰ)求椭圆C的方程;
(Ⅱ)当![]() 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当![]() 、
、![]() 两点在
两点在![]() 上运动,且
上运动,且![]() =6
=6![]() 时,求直线MN的方程.
时,求直线MN的方程.
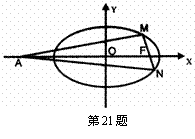 |
解:(Ⅰ)![]() 椭圆的离心率为
椭圆的离心率为![]()
即![]() 可得
可得![]() --2分
--2分
又椭圆![]() 过点P
过点P![]()
![]()
解得![]() ,
,![]() ,椭圆C的方程为
,椭圆C的方程为![]() -----
-----![]() -----------4分
-----------4分
 |
(Ⅱ)设![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() , -----------5分
, -----------5分
由M,N两点在椭圆上,
![]() ---------6分
---------6分
若![]() ,则
,则![]() (舍去),
(舍去),![]() ------------7分
------------7分
![]() . ------------8分
. ------------8分
(Ⅲ)因为![]() =6
=6![]() .--9分
.--9分
由已知点F(2,0), 所以|AF|=6, 即得|yM-yN|=![]() ------------10分
------------10分
当MN![]() 轴时,
轴时,![]() 故直线的斜率存在. ------------11分
故直线的斜率存在. ------------11分
不妨设直线MN的方程为:![]() -----
-----![]()
联立![]() 、
、![]() 得
得![]() ------------12分
------------12分
![]() |
|![]() |=
|=![]() 解得
解得![]() ------------14分
------------14分
此时,直线MN的方程为![]() 或
或![]() ------------15分
------------15分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率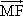 =λ
=λ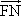 (λ>0),定点A(-4,0).
(λ>0),定点A(-4,0).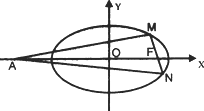
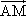 ·
·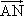 tan∠MAN=6
tan∠MAN=6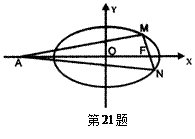 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程; 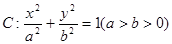 过点P
过点P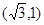 ,且离心率为
,且离心率为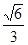 ,F为椭圆的右焦点,
,F为椭圆的右焦点,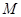 、
、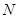 两点在椭圆
两点在椭圆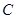 上,且
上,且
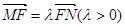 ,定点
,定点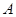 (-4,0).
(-4,0).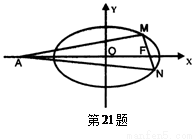
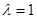 时
,问:MN与AF是否垂直;并证明你的结论.
时
,问:MN与AF是否垂直;并证明你的结论.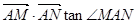 =6
=6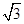 时, 求直线MN的方程.
时, 求直线MN的方程.