题目内容
设函数f(x)=|2x-2|+|x+3|.(1)解不等式f(x)>6;
(2)若关于x的不等式f(x)≤|2a-1|的解集不是空集,试求a的取值范围.
【答案】分析:(1)根据绝对值的代数意义,去掉函数f(x)=|2x-2|+|x+3|中的绝对值符号,求解不等式f(x)>6,
(2)把关于x的不等式f(x)≤|2a-1|的解集不是空集,转化为关于x的不等式f(x)≤|2a-1|的解集非空,求函数f(x)的最小值即可求得a的取值范围.
解答:解:(1)解:f(x)=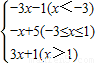
①由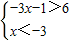 ,解得x<-3;
,解得x<-3;
②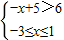 ,解得-3≤x<-1;
,解得-3≤x<-1;
③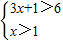 ,解得x>
,解得x> ;
;
综上可知不等式的解集为{x|x> 或x<-1}.
或x<-1}.
(2)因为f(x)=|2x-2|+|x+3|≥4,
所以若f(x)≤|2a-1|的解集不是空集,则|2a-1|≥f(x)min=4,
解得:a≥ 或a≤-
或a≤- ..
..
即a的取值范围是:a≥ 或a≤-
或a≤- .
.
点评:考查了绝对值的代数意义,去绝对值体现了分类讨论的数学思想;根据函数图象求函数的最值,体现了数形结合的思想.属中档题,求解问题(2)体现了转化的数学思想,属中档题.
(2)把关于x的不等式f(x)≤|2a-1|的解集不是空集,转化为关于x的不等式f(x)≤|2a-1|的解集非空,求函数f(x)的最小值即可求得a的取值范围.
解答:解:(1)解:f(x)=
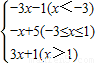
①由
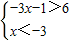 ,解得x<-3;
,解得x<-3;②
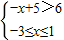 ,解得-3≤x<-1;
,解得-3≤x<-1;③
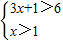 ,解得x>
,解得x> ;
;综上可知不等式的解集为{x|x>
 或x<-1}.
或x<-1}.(2)因为f(x)=|2x-2|+|x+3|≥4,
所以若f(x)≤|2a-1|的解集不是空集,则|2a-1|≥f(x)min=4,
解得:a≥
 或a≤-
或a≤- ..
..即a的取值范围是:a≥
 或a≤-
或a≤- .
.点评:考查了绝对值的代数意义,去绝对值体现了分类讨论的数学思想;根据函数图象求函数的最值,体现了数形结合的思想.属中档题,求解问题(2)体现了转化的数学思想,属中档题.

练习册系列答案
相关题目