题目内容
已知命题p:方程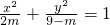 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线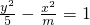 的离心率
的离心率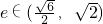 .若p或q为真命题,p且q为假命题,求实数m的取值范围.
.若p或q为真命题,p且q为假命题,求实数m的取值范围.
解:p真,则有9-m>2m>0,即0<m<3…2分
q真,则有m>0,且e2=1+ =1+
=1+ ∈(
∈( ,2),
,2),
即 <m<5…4分
<m<5…4分
若p或q为真命题,p且q为假命题,则p、q一真一假.
①若p真、q假,则0<m<3,且m≥5或m≤ ,即0<m≤
,即0<m≤ ;…6分
;…6分
②若p假、q真,则m≥3或m≤0,且 <m<5,即3≤m<5…8分
<m<5,即3≤m<5…8分
故实数m的取值范围为0<m≤ 或3≤m<5…10分
或3≤m<5…10分
分析:由p真与q真分别求得m的范围,利用复合命题的真假判断即可求得符合题意的实数m的取值范围.
点评:本题考查椭圆与双曲线的简单性质,考查复合命题的真假判断,考查集合的交补运算,属于中档题.
q真,则有m>0,且e2=1+
 =1+
=1+ ∈(
∈( ,2),
,2),即
 <m<5…4分
<m<5…4分若p或q为真命题,p且q为假命题,则p、q一真一假.
①若p真、q假,则0<m<3,且m≥5或m≤
 ,即0<m≤
,即0<m≤ ;…6分
;…6分②若p假、q真,则m≥3或m≤0,且
 <m<5,即3≤m<5…8分
<m<5,即3≤m<5…8分故实数m的取值范围为0<m≤
 或3≤m<5…10分
或3≤m<5…10分分析:由p真与q真分别求得m的范围,利用复合命题的真假判断即可求得符合题意的实数m的取值范围.
点评:本题考查椭圆与双曲线的简单性质,考查复合命题的真假判断,考查集合的交补运算,属于中档题.

练习册系列答案
相关题目
 是“方程
是“方程 ”表示椭圆的充要条件;
”表示椭圆的充要条件; 所表示的点在第二象限;
所表示的点在第二象限; 平面
平面 ,平面
,平面 ,则直线
,则直线 ,则下列复合命题中正确的是( )
,则下列复合命题中正确的是( )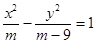 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围.
,若p、q有且只有一个为真,求m的取值范围. 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆; 的离心率
的离心率 ;
; ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围. 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围