题目内容
已知定义在 上的函数
上的函数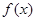 是周期为
是周期为 的偶函数,当
的偶函数,当 时,
时, ,如果直线
,如果直线 与曲线
与曲线 恰有两个交点,则实数
恰有两个交点,则实数 的值是( )
的值是( )
A.
B.
C. 或
或
D. 或
或
【答案】
D
【解析】

试题分析:由题意, 是偶函数,且当
是偶函数,且当 时,
时, ,当
,当 时,
时,
 从而
从而 .
. 是周期为
是周期为 的偶函数,
的偶函数, 当
当 时,
时,
画出函数 的图像,满足线
的图像,满足线 与曲线
与曲线 恰有两个交点,分两类情况:一是直线与一个周期内的抛物线弧相切,然后与另一个周期的抛物线弧相交一个交点,如
恰有两个交点,分两类情况:一是直线与一个周期内的抛物线弧相切,然后与另一个周期的抛物线弧相交一个交点,如 ,
, 与
与 联立方程组,由判别式为0可得
联立方程组,由判别式为0可得 二是与抛物线有两个交点,如
二是与抛物线有两个交点,如 此时直线过原点,故
此时直线过原点,故 结合函数的周期为
结合函数的周期为 ,故答案为D.
,故答案为D.
考点:函数图象及其性质.

练习册系列答案
相关题目
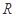 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足 ,且
,且 ,(其中
,(其中 为
为 项和)。则
项和)。则
 B.
B.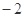 C.
C. D.
D.
 上的函数
上的函数 是偶函数,且
是偶函数,且 时,
时,  ,
, 解析式; (2)写出
解析式; (2)写出 上的函数
上的函数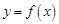 是偶函数,且
是偶函数,且 时,
时,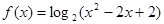 ,
, 时,求
时,求 解析式;
解析式; 上的函数
上的函数 是偶函数,且
是偶函数,且 时,
时, ,
, 时,求
时,求 解析式;
解析式;