题目内容
已知三点：A（4，0），B（0，4），C（3cosα，3sinα）
①若a∈（-π，0），且|
|=|
|，求角α的值；
②若
•
=0，求
①若a∈（-π，0），且|
| AC |
| BC |
②若
| AC |
| BC |
| 2sin2a+sin2a |
| 1+tana |
（1）由已知|
|=|
|代入坐标得：
（3sinα-4）2+（3sinα）2=（3cosα）2+（3sinα-4）2
即sinα=cosα，所以tanα=1，
因为a∈（-π，0），所以α=-
（2）由已知
•
=0代入坐标得：
（3cosα-4，3sinα）•（3cosα，3sinα-4）
=9cos2α-12cosα+9sin2α-12sinα
=9-12（sinα+cosα）=0
所以sinα+cosα=
平方得1+2sinα•cosα=
所以2sinα•cosα=-
又因为
=
=
=2sinα•cosα=-
| AC |
| BC |
（3sinα-4）2+（3sinα）2=（3cosα）2+（3sinα-4）2
即sinα=cosα，所以tanα=1，
因为a∈（-π，0），所以α=-
| 3π |
| 4 |
（2）由已知
| AC |
| BC |
（3cosα-4，3sinα）•（3cosα，3sinα-4）
=9cos2α-12cosα+9sin2α-12sinα
=9-12（sinα+cosα）=0
所以sinα+cosα=
| 3 |
| 4 |
平方得1+2sinα•cosα=
| 9 |
| 16 |
所以2sinα•cosα=-
| 7 |
| 16 |
又因为
| 2sin2a+sin2a |
| 1+tana |
| 2sin2α+2sinαcosα | ||
1+
|
=
| 2sinαcosα(sinα+cosα) |
| sinα+cosα |
| 7 |
| 16 |
练习册系列答案
相关题目
，求角α的值；
，求
，求角α的值；
，求
，求角α的值；
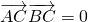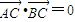，求