题目内容
已知三点:A(4,0),B(0,4),C(3cosα,3sinα)
①若a∈(-π,0),且 ,求角α的值;
,求角α的值;
②若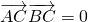 ,求
,求
解:(1)由已知 代入坐标得:
代入坐标得:
(3sinα-4)2+(3sinα)2=(3cosα)2+(3sinα-4)2
即sinα=cosα,所以tanα=1,
因为a∈(-π,0),所以α=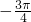
(2)由已知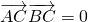 代入坐标得:
代入坐标得:
(3cosα-4,3sinα)•(3cosα,3sinα-4)
=9cos2α-12cosα+9sin2α-12sinα
=9-12(sinα+cosα)=0
所以sinα+cosα=
平方得1+2sinα•cosα=
所以2sinα•cosα=
又因为
= =
=
分析:(1)由已知 代入坐标得出sinα和cosα的关系式,结合α的范围,求出角α的值;
代入坐标得出sinα和cosα的关系式,结合α的范围,求出角α的值;
(2)由已知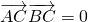 代入坐标得出关于角α的关系式,再将
代入坐标得出关于角α的关系式,再将 利用二倍角公式和切化弦知识统一成角α的关系式,与已知找关系即可.
利用二倍角公式和切化弦知识统一成角α的关系式,与已知找关系即可.
点评:本题是向量和三角的综合问题,以向量的模、向量的数量积为载体考查三角函数的化简和求值运算知识.
 代入坐标得:
代入坐标得:(3sinα-4)2+(3sinα)2=(3cosα)2+(3sinα-4)2
即sinα=cosα,所以tanα=1,
因为a∈(-π,0),所以α=
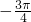
(2)由已知
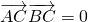 代入坐标得:
代入坐标得:(3cosα-4,3sinα)•(3cosα,3sinα-4)
=9cos2α-12cosα+9sin2α-12sinα
=9-12(sinα+cosα)=0
所以sinα+cosα=

平方得1+2sinα•cosα=

所以2sinα•cosα=

又因为

=
 =
=
分析:(1)由已知
 代入坐标得出sinα和cosα的关系式,结合α的范围,求出角α的值;
代入坐标得出sinα和cosα的关系式,结合α的范围,求出角α的值;(2)由已知
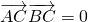 代入坐标得出关于角α的关系式,再将
代入坐标得出关于角α的关系式,再将 利用二倍角公式和切化弦知识统一成角α的关系式,与已知找关系即可.
利用二倍角公式和切化弦知识统一成角α的关系式,与已知找关系即可.点评:本题是向量和三角的综合问题,以向量的模、向量的数量积为载体考查三角函数的化简和求值运算知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求角α的值;
,求角α的值;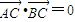 ,求
,求
 ,求角α的值;
,求角α的值; ,求
,求