题目内容
已知参数方程
其中abλ≠0，0≤θ＜2π，在下列条件：（1）t是参数；（2）λ是参数；（3）θ是参数，方程所表示的曲线分别为（ ）
|
| A、（1）（2）（3）均为直线 |
| B、（1）是直线，（2）（3）是圆 |
| C、（2）是直线，（1）（3）是圆 |
| D、（1）（2）是直线，（3）是圆 |
分析：将参数方程分别在条件：（1）t是参数；（2）λ是参数；（3）θ是参数下，消去参数，得到普通方程，根据普通方程判定方程所表示的曲线即可．
解答：解：参数方程
其中abλ≠0，0≤θ＜2π，
（1）t是参数，消去t得
=
即bx-ay+aλsinθ-bλcosθ=0，方程所表示的曲线为直线；
（2）λ是参数，消去λ得，
=
即sinθx-cosθy+btcosθ-atsinθ=0，方程所表示的曲线为直线；
（3）θ是参数，消去θ得，(
)2+(
)2=1即（x-at）2+（y-bt）2=λ2，方程所表示的曲线为圆；
故选D．
|
（1）t是参数，消去t得
| x-λcosθ |
| a |
| y-λsinθ |
| b |
（2）λ是参数，消去λ得，
| x-at |
| cosθ |
| y-bt |
| sinθ |
（3）θ是参数，消去θ得，(
| x-at |
| λ |
| y-bt |
| λ |
故选D．
点评：本题主要考查了参数方程化成普通方程，同时考查了消元、计算的能力和转化的思想，属于基础题．
练习册系列答案
相关题目
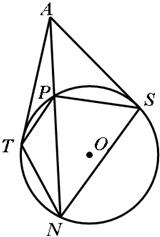选做题A．平面几何选讲
．
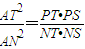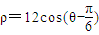上的动点，试求线段AB长的最大值．D．不等式选讲
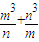≥m2+n2．