题目内容
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
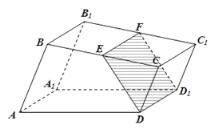
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用面面平行的性质定理得出![]() ,由面面平行的性质定理可得出
,由面面平行的性质定理可得出![]() ,可证明出四边形
,可证明出四边形![]() 为平行四边形,由
为平行四边形,由![]() 平面
平面![]() ,可得出
,可得出![]() ,从而可证明出四边形
,从而可证明出四边形![]() 为矩形;
为矩形;
(2)计算出梯形![]() 的面积和
的面积和![]() 的面积,将梯形
的面积,将梯形![]() 的面积减去
的面积减去![]() 的面积可得出四边形
的面积可得出四边形![]() 的面积,再利用柱体的体积公式可求出几何体
的面积,再利用柱体的体积公式可求出几何体![]() 的体积.
的体积.
(1)在直四棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
在直四棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
在直四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
因此,无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)由于四边形![]() 是直角梯形,且
是直角梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,梯形![]() 的面积为
的面积为![]() ,
,
![]() ,易得
,易得![]() ,
,![]() 的面积为
的面积为![]() ,
,
![]() 四边形
四边形![]() 的面积为
的面积为![]() ,
,
由题意可知,几何体![]() 为直四棱柱,且高为
为直四棱柱,且高为![]() ,
,
因此,几何体![]() 的体积为
的体积为![]() .
.

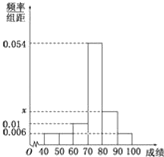
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
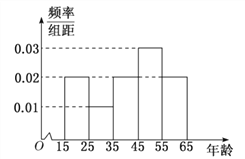
【题目】2019年![]() 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中恰有
人中恰有![]() 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|