题目内容
已知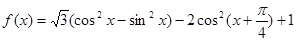 的定义域为[
的定义域为[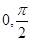 ].
].
(1)求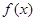 的最小值.
的最小值.
(2)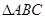 中,
中,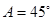 ,
, ,边
,边 的长为函数
的长为函数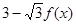 的最大值,求角
的最大值,求角 大小及
大小及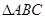 的面积.
的面积.
(1)函数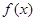 的最小值
的最小值 ;(2)
;(2) 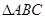 的面积
的面积 .
.
解析试题分析:(1)先化简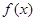 的解析式可得:
的解析式可得:  .将
.将 看作一个整体,根据
看作一个整体,根据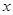 的范围求出
的范围求出 的范围,再利用正弦函数的性质便可得函数
的范围,再利用正弦函数的性质便可得函数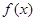 的最小值.(2) 由(1)知函数
的最小值.(2) 由(1)知函数 的最大值
的最大值 ,这样,在
,这样,在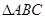 中,便已知了两边及一边的对角,故首先用正弦定理求出另两个角,再用三角形面积公式可得其面积.
中,便已知了两边及一边的对角,故首先用正弦定理求出另两个角,再用三角形面积公式可得其面积.
试题解析:(1)先化简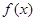 的解析式:
的解析式:


由 ,得
,得 ,
,
所以函数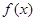 的最小值
的最小值 ,此时
,此时 .
.
(2) 由(1)知函数 的最大值
的最大值 .
.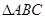 中,
中,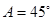 ,
, ,
, ,
,
故 (正弦定理),再由
(正弦定理),再由 知
知 ,故
,故 ,于是
,于是 ,
,
从而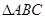 的面积
的面积 .
.
考点:1、三角恒等变形;2、解三角形.

练习册系列答案
相关题目
 分别为△ABC三个内角A、B、C的对边,
分别为△ABC三个内角A、B、C的对边, .
. ,△ABC 的面积为
,△ABC 的面积为 ,求
,求 .
.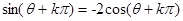
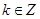
 ;
; 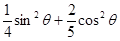
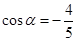 ,
,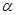 为第三象限角.
为第三象限角.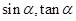 的值;(2)求
的值;(2)求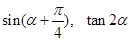 的值.
的值.
 的值,
的值, 的值.
的值.
 中,内角A,B,C所对的边分别为a,b,c,且
中,内角A,B,C所对的边分别为a,b,c,且 .
. ,
, 为
为 的最大值,并指出此时B的值.
的最大值,并指出此时B的值. ,求下列各式的值:
,求下列各式的值: ;
; .
. ,点P,Q分别是在角A的两边上不同于点A的动点.
,点P,Q分别是在角A的两边上不同于点A的动点.
 ,求AQ的长;
,求AQ的长; ,求sin(2α+β)的值.
,求sin(2α+β)的值.