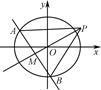
题目内容
已知点 点
点 分别是
分别是 轴和
轴和 轴上的动点,且
轴上的动点,且 ,动点
,动点 满足
满足 ,设动点
,设动点 的轨迹为E.
的轨迹为E.
(1)求曲线E的方程;
(2)点Q(1,a),M,N为曲线E上不同的三点,且 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为 ,求
,求 的最小值.
的最小值.
(1)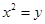 ;(2)
;(2)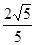 .
.
解析试题分析:(1)设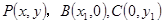 ,利用
,利用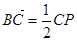 ,用
,用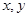 表示
表示 的坐标,然后利用
的坐标,然后利用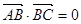 ,得到
,得到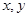 的方程,得到
的方程,得到 点轨迹;
点轨迹;
(2)解法一:利用曲线方程 ,求出
,求出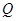 点坐标,设
点坐标,设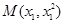 ,
,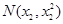 ,
,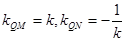 ,通过联立方程,得到
,通过联立方程,得到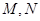 的坐标,利用导数,列出过点
的坐标,利用导数,列出过点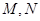 的切线方程,解出点
的切线方程,解出点 的坐标,然后再求
的坐标,然后再求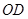 的最小值,
的最小值,
解法二:利用导数,列出过点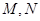 的切线方程,解出点
的切线方程,解出点 的坐标,然后结合
的坐标,然后结合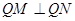 ,能够得到关于点
,能够得到关于点 所满足的方程,再求出
所满足的方程,再求出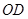 的最小值.
的最小值.
试题解析:(1)解:设
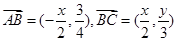 ,由
,由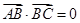 得
得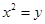 4分
4分
(2)解法一:易知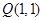 ,设
,设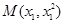 ,
,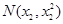 ,
,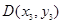 ,
,
设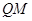 的方程为
的方程为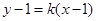
联立方程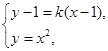 消去
消去 ,得
,得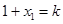 ,所以
,所以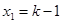 .
.
同理,设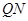 的方程为
的方程为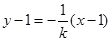 ,
,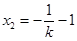 . 6分
. 6分
对函数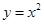 求导,得
求导,得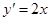 ,
,
所以抛物线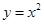 在点
在点 处的切线斜率为
处的切线斜率为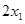 ,
,
所以切线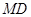 的方程为
的方程为 ,即
,即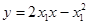 .
.
同理,抛物线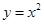 在点
在点 处的切线
处的切线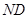 的方程为
的方程为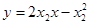 . 8分
. 8分
联立两条切线的方程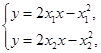
解得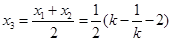 ,
,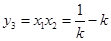 ,
,
所以点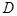 的坐标为
的坐标为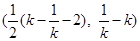 .因此点
.因此点 在直线
在直线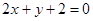 上. 10分
上. 10分
因为点 到直线
到直线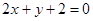 的距离
的距离 ,
,
所以 ,当且仅当点
,当且仅当点 时等号成立.
时等号成立.
由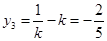 ,得
,得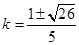 ,验证知符合题意.
,验证知符合题意.
所以当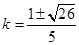 时,
时, 有最小值
有最小值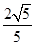 . 12分
. 12分
解法二:由题意,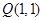 ,设
,设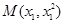 ,
,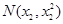 ,
,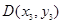 ,
,
对函数

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
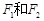 ,且点
,且点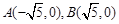 在椭圆C上,又
在椭圆C上,又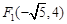 .
.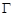 的方程;
的方程;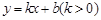 与曲线
与曲线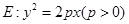 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆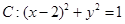 的两条切线,切点为A、B,
的两条切线,切点为A、B,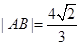 .
.
 与分别在
与分别在 轴、
轴、 轴上的动点
轴上的动点 满足:
满足: ,动点
,动点 满足
满足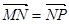 .
. 两点,直线
两点,直线 与直线
与直线 分别交于点
分别交于点 (
( 为坐标原点);
为坐标原点); 为直径的圆的位置关系;
为直径的圆的位置关系; 是否为定值?并证明你的结论.
是否为定值?并证明你的结论. 的左右焦点分别为
的左右焦点分别为 、
、 ,短轴两个端点为
,短轴两个端点为 、
、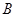 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形. 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点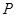 ,证明:
,证明: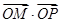 为定值;
为定值; 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线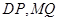 的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
的交点?若存在,求出点Q的坐标;若不存在,请说明理由. 中,已知
中,已知 ,
, ,
, 是椭圆
是椭圆 上不同的三点,
上不同的三点,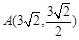 ,
, ,
, 的中点在直线
的中点在直线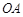 上.
上.
 在椭圆上(异于点
在椭圆上(异于点 ,
, 两点,证明
两点,证明 为定值并求出该定值.
为定值并求出该定值. 的离心率为
的离心率为 ,过左焦点
,过左焦点 且斜率为
且斜率为 的直线交椭圆E于A,B两点,线段AB的中点为M,直线
的直线交椭圆E于A,B两点,线段AB的中点为M,直线 :
: 交椭圆E于C,D两点.
交椭圆E于C,D两点.
 经过点
经过点 ,其左、右顶点分别是
,其左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 ,
, (异于
(异于 交直线
交直线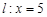 于
于 、
、 两点,若
两点,若 成等比数列.
成等比数列.
 为直径的圆过点
为直径的圆过点 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.