题目内容
8.关于x的方程$x+m=3-\sqrt{4x-{x^2}}$有且只有一个实根,则实数m的取值范围是-1<m≤3或m=1-2$\sqrt{2}$.分析 问题转化为函数y=$\sqrt{4x-{x}^{2}}$与函数y=3-m-x的图象有且只有一个交点,作图求解即可.
解答 解:∵关于x的方程$x+m=3-\sqrt{4x-{x^2}}$有且只有一个实根,
∴函数y=$\sqrt{4x-{x}^{2}}$与函数y=3-m-x的图象有且只有一个交点,
作函数y=$\sqrt{4x-{x}^{2}}$与函数y=3-m-x的图象如下,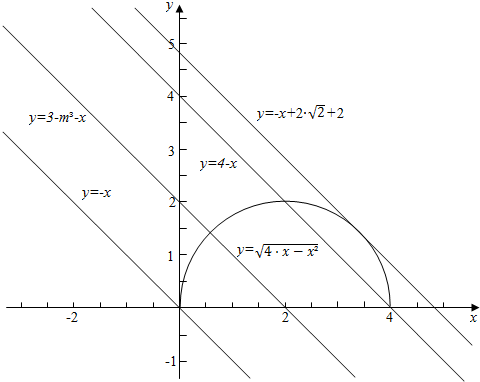
结合图象可知,
0≤3-m<4或3-m=2$\sqrt{2}$+2,
即-1<m≤3或m=1-2$\sqrt{2}$;
故答案为:-1<m≤3或m=1-2$\sqrt{2}$.
点评 本题考查了函数的图象与方程的根的关系应用及数形结合的思想应用,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
18.若函数f(x)是定义R上的增函数,切满足f(1)=0,f(a)+f(b)=f(a+b)-1,那么f(2)=1,关于x的不等式f(x2-1)+f(1-x)>0的解集是(-∞,-1)∪(2,+∞).
20.若${C}_{4}^{x}$+${C}_{4}^{x+1}$=5,则x=( )
| A. | 0或3 | B. | 0 | C. | 3 | D. | 2 |
 如图,已知点S(0,3),SA,SB与圆C:x2+y2-my=0(m>0)和抛物线x2=-2py(p>0)都相切,切点分别为M,N和A,B,SA∥ON,$\overrightarrow{AB}$=λ$\overrightarrow{MN}$,则实数λ的值为( )
如图,已知点S(0,3),SA,SB与圆C:x2+y2-my=0(m>0)和抛物线x2=-2py(p>0)都相切,切点分别为M,N和A,B,SA∥ON,$\overrightarrow{AB}$=λ$\overrightarrow{MN}$,则实数λ的值为( )