题目内容

函数f（x）=tan（x-
π4
）=-1，则 x=
 
．
分析：由 函数f（x）=tan（x-
π
4
）=-1，可得 x-
π
4
=kπ-
π
4
，解出x．
解答：解：∵函数f（x）=tan（x-
π
4
）=-1，∴x-
π
4
=kπ-
π
4
，∴x=kπ-
π
4
，k∈z．
故答案为 kπ，k∈Z．
点评：本题考查根据正切函数的值求角，终边相同的角的表示方法，得到x-
π
4
=kπ-
π
4
，k∈z，是解题的关键．
练习册系列答案
相关题目
有以下四个命题：
①函数f（x）=sin（
π
3
-2x）的一个增区间是[
5π
12
，
11π
12
]；
②若函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍；
③对于函数f（x）=tan（2x+
π
3
），若f（x1）=f（x2），则x1-x2必是π的整数倍；
④函数y=2sin（2x+
π
3
）的图象关于点（
π
3
，0）对称．
其中正确的命题是
 
．（填上正确命题的序号）
设函数f（x）=tan（ωx+?），（ω＞0），条件P：“f（0）=0”；条件Q：“f（x）为奇函数”，则P是Q的（　　）
（2012•南京二模）下列四个命题
①“?x∈R，x2-x+1≤1”的否定；
②“若x2+x-6≥0，则x＞2”的否命题；
③在△ABC中，“A＞30°“sinA＞
12
”的充分不必要条件；
④“函数f（x）=tan（x+φ）为奇函数”的充要条件是“φ=kπ（k∈z）”．
其中真命题的序号是
②
②
．（把真命题的序号都填上）
已知函数f（x）=tan（2x+
π
4
）
（I）求该函数的定义域，周期及单调区间；
（II）若f（θ）=
1
7
，求
2cos2
θ
2
-sinθ-1
2
sin(θ+
π
4
)
的值．
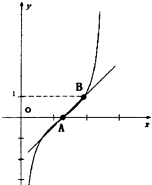精英家教网如图为函数f（x）=tan（
π
4
x-
π
2
）的部分图象，点A为函数f（x）在y轴右侧的第一个零点，点B在函数f（x）图象上，它的纵坐标为1，直线AB的倾斜角等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网