题目内容
设对于不大于![]() 的所有正实数a,如果满足不等式|x一a|<b的一切实数x,亦满足不等式|x-a2|<
的所有正实数a,如果满足不等式|x一a|<b的一切实数x,亦满足不等式|x-a2|<![]() ,求实数b的取值范围.
,求实数b的取值范围.
答案:
解析:
解析:
|
解析:设A={x||x-a|<6=,B={x||x-a2|< 故A=(a-b,a+b),B=(a2- 由题设知A 即b≤-a2+a+ 由-a2+a+ 由a2-a+ ∴ 因此正实数b的取值范围是 点评:本例应注意集合包含关系在解不等式中的运用及函数思想的渗透. |

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 必须成立.
必须成立. 的所有正实数
的所有正实数 ,如果满足不等式
,如果满足不等式 的一切实数
的一切实数 ,也满足不等式
,也满足不等式 ,求实数
,求实数 的取值范围。
的取值范围。 的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式
的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式 ,求实数b的取值范围.
,求实数b的取值范围. 的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式
的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式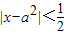 ,求实数b的取值范围.
,求实数b的取值范围.