题目内容
设对于不大于
的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式|x-a2|<
,求实数b的取值范围.
| 5 |
| 4 |
| 1 |
| 2 |
分析:由题意可得b>0,求出这两个不等式的解集,由题意可得 a2-
≤a-b,且 a+b≤a2+
,0<a≤
.由此可得b小于或等于-a2+a+
的最小值,且b小于或等于 a2-a+
的最小值,由此求得实数b的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意可得b>0是不用求的,否则|x-a|<b都没解了.
故有-b<x-a<b,即a-b<x<a+b.
由不等式|x-a2|<
可得,-
<x-a2<
,即 a2-
<x<a2+
.
第二个不等式的范围要大于第一个不等式,这样只要满足了第一个不等式,
肯定满足第二个不等式,命题成立.
故有 a2-
≤a-b,且 a+b≤a2+
,0<a≤
.
化简可得 b≤-a2+a+
,且b≤a2-a+
.
由于-a2+a+
=-(a-
)2+
∈[
,
],故 b≤
.
由于 a2-a+
=(a-
)2+
∈[
,
].故 b≤
.
综上可得 0<b≤
.
故有-b<x-a<b,即a-b<x<a+b.
由不等式|x-a2|<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
第二个不等式的范围要大于第一个不等式,这样只要满足了第一个不等式,
肯定满足第二个不等式,命题成立.
故有 a2-
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
化简可得 b≤-a2+a+
| 1 |
| 2 |
| 1 |
| 2 |
由于-a2+a+
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |
| 16 |
由于 a2-a+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 13 |
| 16 |
| 1 |
| 4 |
综上可得 0<b≤
| 3 |
| 16 |
点评:本题主要考查绝对值不等式的解法,求二次函数在闭区间上的值域,函数的恒成立问题,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 的所有正实数
的所有正实数 ,如果满足不等式
,如果满足不等式 的一切实数
的一切实数 ,也满足不等式
,也满足不等式 ,求实数
,求实数 的取值范围。
的取值范围。 的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式
的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式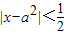 ,求实数b的取值范围.
,求实数b的取值范围.