题目内容
已知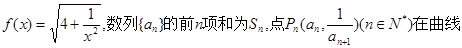
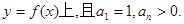
(1)求数列{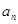 }的通项公式
}的通项公式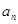
(2)数列{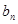 }的首项b1=1,前n项和为Tn,且
}的首项b1=1,前n项和为Tn,且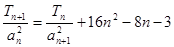 ,求数列{
,求数列{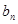 }
}
的通项公式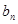 .
.
(1) ;(2)
;(2) 。
。
解析试题分析:(1)由题意知 ………………2分
………………2分
 是等差数列.…………………………4分
是等差数列.…………………………4分
 ………5分
………5分 ………………………………6分
………………………………6分
(2)由题设知

 是等差数列. …………………………………8分
是等差数列. …………………………………8分
 …………………………10分
…………………………10分
∴当n=1时, ;
;
当
经验证n=1时也适合上式.  ……………12分
……………12分
考点:等差数列的定义;通项公式的求法;
点评:在求数列的通项公式时,常用的一种方法是构造新数列,通过构造的新数列是等差数列或等比数列来求。比如此题,要求数列{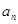 }的通项公式我们构造了数列
}的通项公式我们构造了数列 是等差数列。想求
是等差数列。想求 的通项公式,构造了
的通项公式,构造了 是等差数列。
是等差数列。

练习册系列答案
相关题目
在数列{an}中,a1=1,an+1-an=n(n∈N*),则a100的值为( )
| A.5 050 | B.5 051 | C.4 950 | D.4 951 |
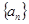 的首项
的首项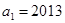 ,公比
,公比 ,数列
,数列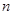 项的积记为
项的积记为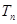 .
.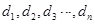 ,证明:数列
,证明:数列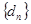 为等比数列.
为等比数列.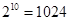 )
) }满足
}满足 。
。 }是等比数列。
}是等比数列。 满足:
满足:
 为等比数列;
为等比数列; 为递增数列;
为递增数列; 的取值范围。
的取值范围。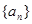 ,
,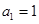 ,
,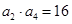 ,单调增数列
,单调增数列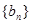 的前
的前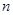 项和为
项和为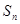 ,
,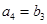 ,且
,且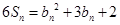 (
(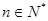 ).
).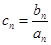 (
(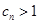 的所有
的所有 中,
中,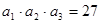 ,
,
 (2)求出
(2)求出
 的公差
的公差 ,设
,设 ,
,
 ,求数列
,求数列 ,且
,且 成等比数列,求
成等比数列,求 的值;
的值; ,证明:
,证明: .
. 的前n项和记为
的前n项和记为 ,已知
,已知  .
. ;
;